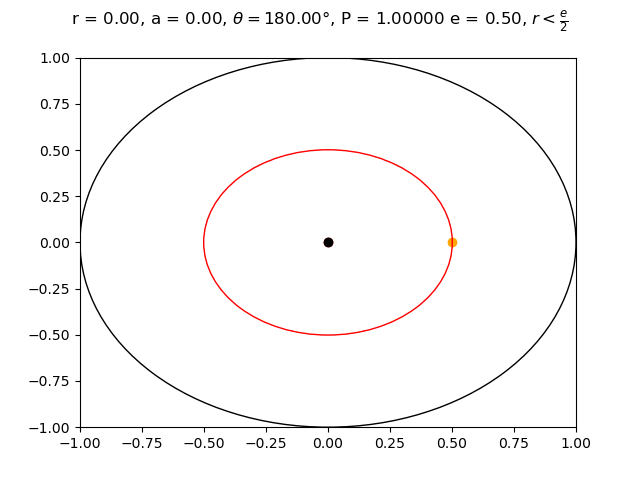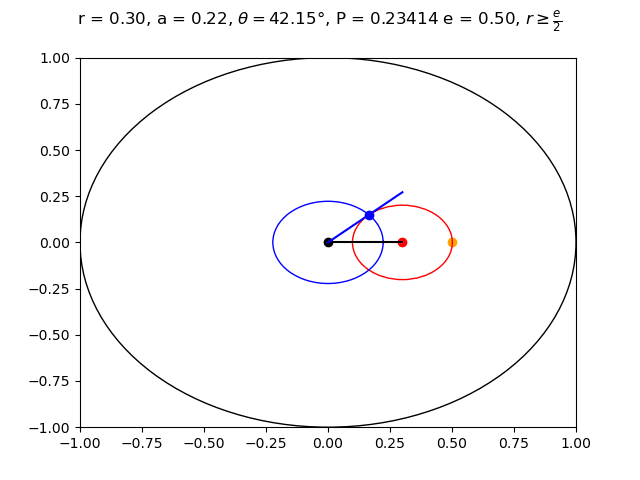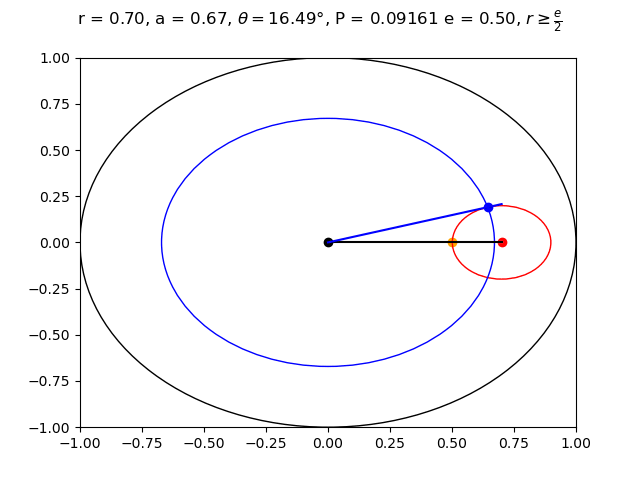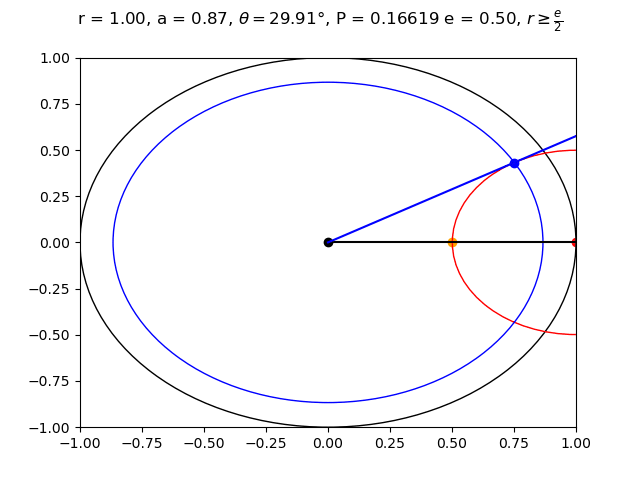
Suppose the flag is placed at polar coordinate $(r, \theta)$.
Let $e$ represent the fixed distance that Erin chooses along $\theta$.
Let $a$ represent the radius that Aaron chooses.
Erin will choose point $(e, \theta)$. This means that she will be a distance of $|r - e|$ away from the flag.
For symmetry reasons we can assume that $\theta = 0$, meaning that the flag is placed at $(r, 0)$. Then Aaron will beat Erin if his point is within the circle $(x - r)^2 + y^2 = (r - e)^2$. Let us call this circle $E$.
Since Aaron does not know $\theta$, the range of points that Aaron can pick lie on the outline of the circle $x^2 + y^2 = a^2$. Let us call this circle $A$. The probability that Aaron wins at a specific value of $a$, $e$, and $r$ is equal to the fraction of the outline of circle $A$ that is contained within circle $E$, since any $\theta$ has an equal chance of being correct. We can calculate this by looking at the angle at which these two circles intersect. Then the probability that Aaron wins will be this angle divided by $2 \pi $. To make things easier we can just look at the top half of the circle, and get the angle from line $y = 0$ to the intersection of these circles, and divide by $\pi$. Our goal now is to maximize this angle.
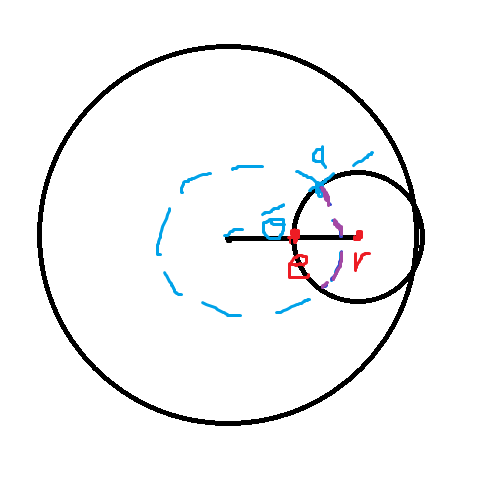
Let the point at which these circles intersect be at $(x, y) = (a \cos \theta, a \sin \theta)$. Plugging this into the equation for circle $E$ we get $(a \cos \theta - r)^2 + (a \sin \theta)^2 = (r - e)^2$. Rearranging this gets us that $\theta = \cos^{-1}(\frac{a^2 + 2er - e^2}{2ar})$. Now we want to find an equation for $a$ that maximizes $\theta$ between $0 \leq a \leq 1$.
$\theta' = 0$ when $a = \sqrt{2er - e^2}$. This gives us the maximum $\theta$ value. Note that $2er - e^2 \geq 0$ only when $r \geq \frac{e}{2}$. When $r < \frac{e}{2}$ the maximum value of $\theta$ occurs at endpoint $a = 0$. This makes sense because if $r < \frac{e}{2}$, then Erin will be a distance greater than $\frac{e}{2}$ away from the flag, while if Aaron chooses $(0, 0)$ then he will be a distance less than $\frac{e}{2}$ away from the flag and be guaranteed to win. It was a little surprising to me that even though Aaron is given radius $r$, he actually chooses a smaller radius to maximize his winning probability.
We can also check that $a \leq r$ to make sure that we don't go outside of the bounds set for us. This gets us condition $(r - e)^2 \geq 0$ which always holds true.
Plugging $a = \sqrt{2er - e^2}$ into our equation for $\theta$ we get that $\theta = \cos^{-1}(\frac{\sqrt{2er - e^2}}{r})$.
Remember that we are only considering the top half of the circle.
$$\begin{gather}
P(\text{Aaron winning}) = \frac{\frac{1}{2} \pi (\frac{e}{2})^2 + \int_{\frac{e}{2}}^1 \int_0^{\cos^{-1}(\frac{\sqrt{2er - e^2}}{r})}r d \theta dr}{\frac{1}{2} \pi (1)^2} \\\
= (\frac{e}{2})^2 + \frac{2}{\pi} \int_{\frac{e}{2}}^1 \int_0^{\cos^{-1}(\frac{\sqrt{2er - e^2}}{r})}r d \theta dr \\\
P(\text{Aaron winning}) = (\frac{e}{2})^2 + \frac{2}{\pi} \int_{\frac{e}{2}}^1 r \cos^{-1}(\frac{\sqrt{2er - e^2}}{r}) dr
\end{gather}$$
At this point my solution becomes pretty identical to the official solution. If you use $\sin(\cos^{-1}(x)) = \sqrt{1 - x^2}$ you can get that $\cos^{-1}(\frac{\sqrt{2er - e^2}}{r}) = \sin^{-1}(\frac{|r - e|}{r})$ which is the formula used in the official solution. I did not think to draw the triangle in the official solution which would have gotten me this equation quicker.
With Erin knowing that $P(e) = (\frac{e}{2})^2 + \frac{2}{\pi} \int_{\frac{e}{2}}^1 r \cos^{-1}(\frac{\sqrt{2er - e^2}}{r}) dr$ she will try to choose a value of $e$ that minimizes the value of this equation.
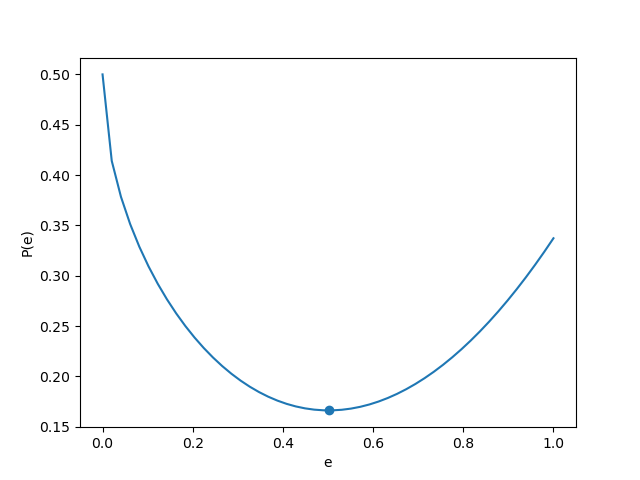
Since this graph is simple enough, we can just use scipy to find the minimum instead of taking the integral with respect to $r$ and derivative with respect to $e$. This gets us that the minimum value of $e$ occurs at $e \approx 0.5013069457$ with $P(e) \approx 0.1661864864$
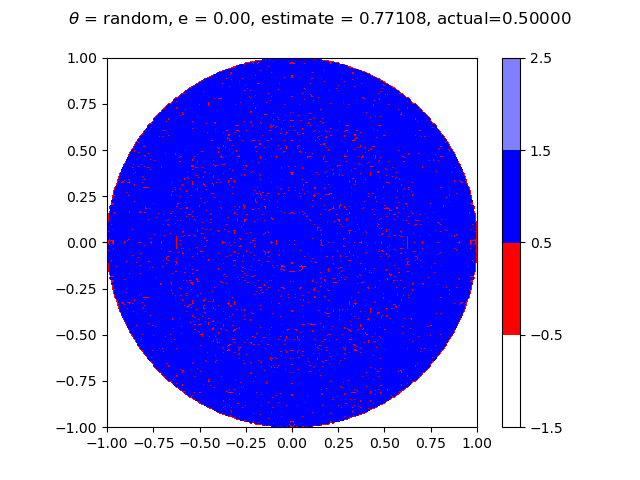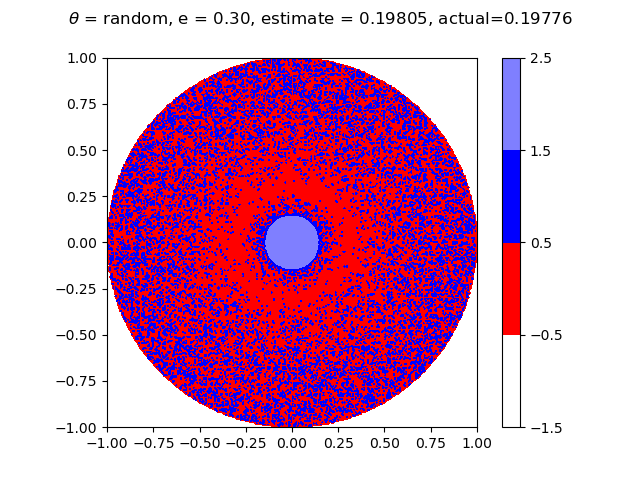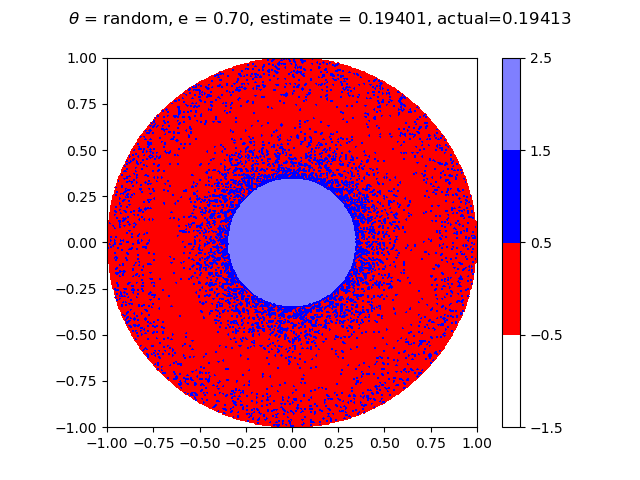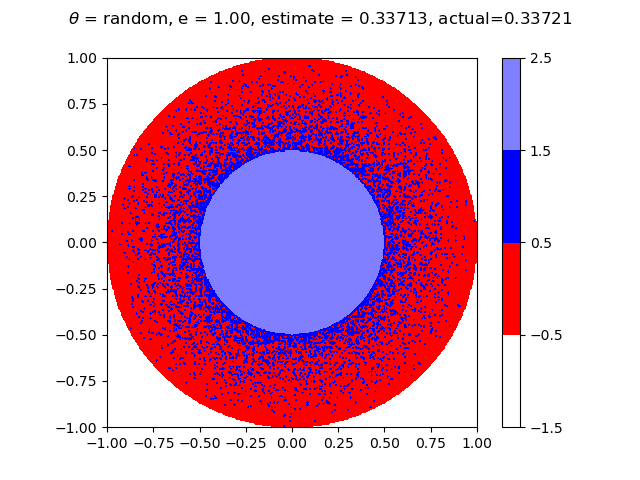
Below are graphs at different values of $e$ showing what the result would be with the flag placed at every point in the circle. The estimate is Aaron's winning probability based on these graphs, while actual is this probability based off of the equations. The graph on the left has Aaron choosing polar coordinate $(a, 0)$, and the graph on the right has Aaron choosing a random value for $\theta$. Both should result in the same winning percentage. Aaron wins at the blue points and loses at the red points. He chooses $a = 0$ at the lighter shades of blue and $a = \sqrt{2er - e^2}$ otherwise.
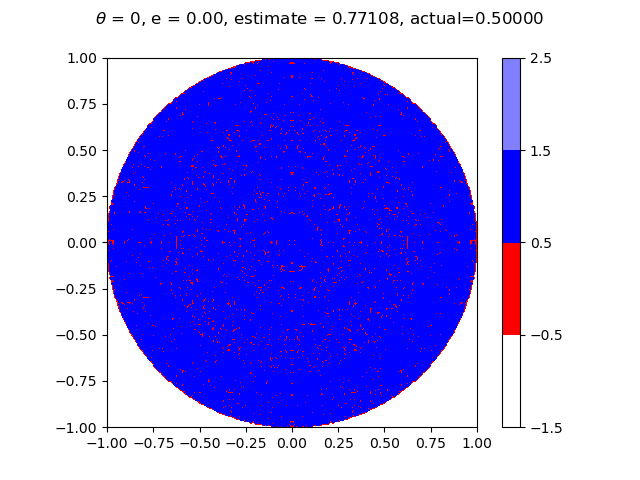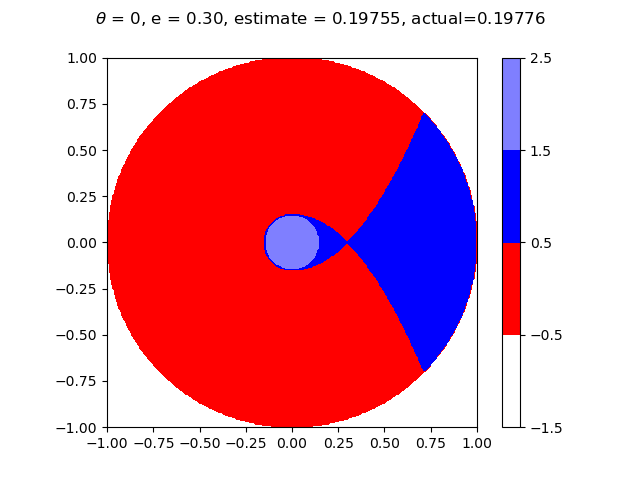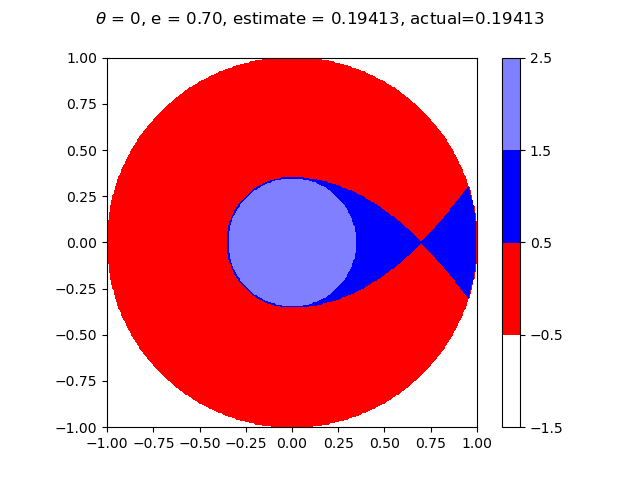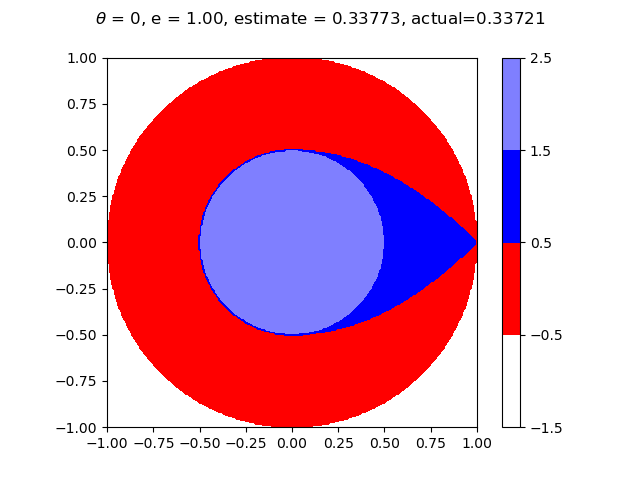
Finally, similar to the image at the top, below is a graph showing the size of the radius $a$ that Aaron chooses as a function of chosen radius $r$, along with Aaron's probability of winning at this value of $r$, with $e \approx 0.5013069457$