■ Study-Algorithm Kyungpook National University
- 해당 Repository에 있는 소스코드들에 대한 문제에 대한 저작권은 알고리즘 문제 사이트에 귀속되어 있습니다.
- 수학에서, 자연수의 계승(階乘, 문화어: 차례곱, 영어: factorial 팩토리얼[*])은 그 수보다 작거나 같은 모든 양의 정수의 곱이다. n이 하나의 자연수일 때, 1에서 n까지의 모든 자연수의 곱을 n에 상대하여 이르는 말이다. 기호는 !을 쓰며 팩토리얼이라고 읽는다. 팩토리얼을 줄여서 팩이라고 읽기도 한다.
#define LONG long long
LONG factorial(int index) {
if (index <= 1) { return 1; }
// Memorization
if (answer[index] > 1) { return answer[index]; }
answer[index] = index * factorial(index - 1);
return answer[index];
}- 수론에서, 정수들의 공약수(公約數, 영어: common divisor)는 동시에 그들 모두의 약수인 정수다. 적어도 하나가 0이 아닌 정수들의 최대공약수(最大公約數, 문화어: 련속나눔셈; 영어: greatest common divisor, 약자 GCD)는 공약수 가운데 가장 큰 하나다. 다항식이나 환의 원소에 대해서도 정의할 수 있다.
/* Reculsive greatest Common Divisor - (logN) */
int GCD(int a, int b) {
if (b == 0) { return a; }
else { return GCD(b, a%b); }
}
/* Loop greatest Common Divisor - (logN) */
int GCD(int a, int b) {
while (b != 0) {
const int r = a % b;
a = b;
b = r;
}
return a;
}- 수학에서 에라토스테네스의 체는 소수를 찾는 방법이다. 고대 그리스 수학자 에라토스테네스가 발견하였다.
-
2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
-
2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
-
자기 자신을 제외한 2의 배수를 모두 지운다.
-
남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
-
자기 자신을 제외한 3의 배수를 모두 지운다.
-
남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
-
자기 자신을 제외한 5의 배수를 모두 지운다.
-
남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
-
자기 자신을 제외한 7의 배수를 모두 지운다.
-
위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다.
/* Sieve of Eratoshenes */
void SoE(const int n, const int m) {
int pn = 0; // 소수의 개수
vector<int> prime; // 소수 저장
vector<bool> check = vector<bool>(n + 1, false); // 소수 확인
for (long long ii = 2; ii <= n; ii++) {
if (check.at(ii) == false) {
pn++;
prime.push_back(ii);
for (long long jj = ii * ii; jj <= n; jj += ii) {
check[jj] = true;
}
}
}
}- 대칭수(對稱數) 또는 회문수(回文數)는 순서대로 읽은 수와 거꾸로 읽은 수가 일치하는 수를 말한다. 예를 들면 34543은 대칭수이고, 34567은 대칭수가 아니다. 컴퓨터 학자 그루엔버거(F.Gruenberger)는 1984년에 미국의 잡지〈사이언티픽 아메리칸〉에 싣게 된 ‘컴퓨터 레크리에이션’이라는 칼럼에서 이와 같은 흥미로운 알고리즘을 제시해서 많은 사람의 이목을 끌었다. 2002는 2와 2, 0과 0의 위치를 바꿔도 대칭수이다.
#define STRING_PAIR pair<string, string>
// Under 100,000,000 List
vector<int> palindrome = {2,3,5,7,11,101,131,151,181,191,313,353,373,383,727,757,787,797,919,929,10301,10501,10601,11311,11411,12421,12721,12821,13331,13831,13931,14341,14741,15451,15551,16061,16361,16561,16661,17471,17971,18181,18481,19391,19891,19991,30103,30203,30403,30703,30803,31013,31513,32323,32423,33533,34543,34843,35053,35153,35353,35753,36263,36563,37273,37573,38083,38183,38783,39293,70207,70507,70607,71317,71917,72227,72727,73037,73237,73637,74047,74747,75557,76367,76667,77377,77477,77977,78487,78787,78887,79397,79697,79997,90709,91019,93139,93239,93739,94049,94349,94649,94849,94949,95959,96269,96469,96769,97379,97579,97879,98389,98689,1003001,1008001,1022201,1028201,1035301,1043401,1055501,1062601,1065601,1074701,1082801,1085801,1092901,1093901,1114111,1117111,1120211,1123211,1126211,1129211,1134311,1145411,1150511,1153511,1160611,1163611,1175711,1177711,1178711,1180811,1183811,1186811,1190911,1193911,1196911,1201021,1208021,1212121,1215121,1218121,1221221,1235321,1242421,1243421,1245421,1250521,1253521,1257521,1262621,1268621,1273721,1276721,1278721,1280821,1281821,1286821,1287821,1300031,1303031,1311131,1317131,1327231,1328231,1333331,1335331,1338331,1343431,1360631,1362631,1363631,1371731,1374731,1390931,1407041,1409041,1411141,1412141,1422241,1437341,1444441,1447441,1452541,1456541,1461641,1463641,1464641,1469641,1486841,1489841,1490941,1496941,1508051,1513151,1520251,1532351,1535351,1542451,1548451,1550551,1551551,1556551,1557551,1565651,1572751,1579751,1580851,1583851,1589851,1594951,1597951,1598951,1600061,1609061,1611161,1616161,1628261,1630361,1633361,1640461,1643461,1646461,1654561,1657561,1658561,1660661,1670761,1684861,1685861,1688861,1695961,1703071,1707071,1712171,1714171,1730371,1734371,1737371,1748471,1755571,1761671,1764671,1777771,1793971,1802081,1805081,1820281,1823281,1824281,1826281,1829281,1831381,1832381,1842481,1851581,1853581,1856581,1865681,1876781,1878781,1879781,1880881,1881881,1883881,1884881,1895981,1903091,1908091,1909091,1917191,1924291,1930391,1936391,1941491,1951591,1952591,1957591,1958591,1963691,1968691,1969691,1970791,1976791,1981891,1982891,1984891,1987891,1988891,1993991,1995991,1998991,3001003,3002003,3007003,3016103,3026203,3064603,3065603,3072703,3073703,3075703,3083803,3089803,3091903,3095903,3103013,3106013,3127213,3135313,3140413,3155513,3158513,3160613,3166613,3181813,3187813,3193913,3196913,3198913,3211123,3212123,3218123,3222223,3223223,3228223,3233323,3236323,3241423,3245423,3252523,3256523,3258523,3260623,3267623,3272723,3283823,3285823,3286823,3288823,3291923,3293923,3304033,3305033,3307033,3310133,3315133,3319133,3321233,3329233,3331333,3337333,3343433,3353533,3362633,3364633,3365633,3368633,3380833,3391933,3392933,3400043,3411143,3417143,3424243,3425243,3427243,3439343,3441443,3443443,3444443,3447443,3449443,3452543,3460643,3466643,3470743,3479743,3485843,3487843,3503053,3515153,3517153,3528253,3541453,3553553,3558553,3563653,3569653,3586853,3589853,3590953,3591953,3594953,3601063,3607063,3618163,3621263,3627263,3635363,3643463,3646463,3670763,3673763,3680863,3689863,3698963,3708073,3709073,3716173,3717173,3721273,3722273,3728273,3732373,3743473,3746473,3762673,3763673,3765673,3768673,3769673,3773773,3774773,3781873,3784873,3792973,3793973,3799973,3804083,3806083,3812183,3814183,3826283,3829283,3836383,3842483,3853583,3858583,3863683,3864683,3867683,3869683,3871783,3878783,3893983,3899983,3913193,3916193,3918193,3924293,3927293,3931393,3938393,3942493,3946493,3948493,3964693,3970793,3983893,3991993,3994993,3997993,3998993,7014107,7035307,7036307,7041407,7046407,7057507,7065607,7069607,7073707,7079707,7082807,7084807,7087807,7093907,7096907,7100017,7114117,7115117,7118117,7129217,7134317,7136317,7141417,7145417,7155517,7156517,7158517,7159517,7177717,7190917,7194917,7215127,7226227,7246427,7249427,7250527,7256527,7257527,7261627,7267627,7276727,7278727,7291927,7300037,7302037,7310137,7314137,7324237,7327237,7347437,7352537,7354537,7362637,7365637,7381837,7388837,7392937,7401047,7403047,7409047,7415147,7434347,7436347,7439347,7452547,7461647,7466647,7472747,7475747,7485847,7486847,7489847,7493947,7507057,7508057,7518157,7519157,7521257,7527257,7540457,7562657,7564657,7576757,7586857,7592957,7594957,7600067,7611167,7619167,7622267,7630367,7632367,7644467,7654567,7662667,7665667,7666667,7668667,7669667,7674767,7681867,7690967,7693967,7696967,7715177,7718177,7722277,7729277,7733377,7742477,7747477,7750577,7758577,7764677,7772777,7774777,7778777,7782877,7783877,7791977,7794977,7807087,7819187,7820287,7821287,7831387,7832387,7838387,7843487,7850587,7856587,7865687,7867687,7868687,7873787,7884887,7891987,7897987,7913197,7916197,7930397,7933397,7935397,7938397,7941497,7943497,7949497,7957597,7958597,7960697,7977797,7984897,7985897,7987897,7996997,9002009,9015109,9024209,9037309,9042409,9043409,9045409,9046409,9049409,9067609,9073709,9076709,9078709,9091909,9095909,9103019,9109019,9110119,9127219,9128219,9136319,9149419,9169619,9173719,9174719,9179719,9185819,9196919,9199919,9200029,9209029,9212129,9217129,9222229,9223229,9230329,9231329,9255529,9269629,9271729,9277729,9280829,9286829,9289829,9318139,9320239,9324239,9329239,9332339,9338339,9351539,9357539,9375739,9384839,9397939,9400049,9414149,9419149,9433349,9439349,9440449,9446449,9451549,9470749,9477749,9492949,9493949,9495949,9504059,9514159,9526259,9529259,9547459,9556559,9558559,9561659,9577759,9583859,9585859,9586859,9601069,9602069,9604069,9610169,9620269,9624269,9626269,9632369,9634369,9645469,9650569,9657569,9670769,9686869,9700079,9709079,9711179,9714179,9724279,9727279,9732379,9733379,9743479,9749479,9752579,9754579,9758579,9762679,9770779,9776779,9779779,9781879,9782879,9787879,9788879,9795979,9801089,9807089,9809089,9817189,9818189,9820289,9822289,9836389,9837389,9845489,9852589,9871789,9888889,9889889,9896989,9902099,9907099,9908099,9916199,9918199,9919199,9921299,9923299,9926299,9927299,9931399,9932399,9935399,9938399,9957599,9965699,9978799,9980899,9981899,9989899};
void setPalindrome(const int prime) {
STRING_PAIR comp = make_pair(string(), string());
comp.first = comp.second = to_string(prime);
reverse(comp.second.begin(), comp.second.end());
if (comp.first == comp.second) { palindrome.push_back(prime); }
}- 골드바흐의 추측(Goldbach's conjecture)은 오래전부터 알려진 정수론의 미해결 문제로, 2보다 큰 모든 짝수는 두 개의 소수(Prime number)의 합으로 표시할 수 있다는 것이다. 이때 하나의 소수를 두 번 사용하는 것은 허용한다.
void goldbach(int number) {
for (int ii = 0; ii < length; ii++) {
int var = number - prime[ii];
if (!check[var] && number == var + prime[ii]) {
printf("%d = %d + %d\n", number, prime[ii], var);
return;
}
}
printf("Goldbach's conjecture is wrong.\n");
}- 무차별 대입 공격(영어: brute force attack)은 특정한 암호를 풀기 위해 가능한 모든 값을 대입하는 것을 의미한다. 대부분의 암호화 방식은 이론적으로 무차별 대입 공격에 대해 안전하지 못하며, 충분한 시간이 존재한다면 암호화된 정보를 해독할 수 있다. 하지만 대부분의 경우 모든 계산을 마치려면 실용적이지 못한 비용이나 시간을 소요하게 되어, 공격을 방지하게 한다. 암호의 '취약점'이라는 의미에는 무차별 대입 공격보다 더 빠른 공격 방법이 존재한다는 것을 의미한다.
- In computer science, a mask is data that is used for bitwise operations, particularly in a bit field. Using a mask, multiple bits in a byte, nibble, word etc. can be set either on, off or inverted from on to off (or vice versa) in a single bitwise operation.
bool mask(int number, const int target) {
int bit = (1 << target);
return (number & bit) == bit; // Duplicate True
// ※ INSERT -> number |= bit
// ※ DELETE and Toggle -> number ^= bit
}- 서로 다른 nn개의 원소에서 rr개를 중복없이 골라 순서에 상관있게 나열하는 것을 nn개에서 rr개를 택하는 순열이라고 한다.
#define SWAP(X, Y, Z) Z=X; X=Y; Y=Z;
bool nextPermutation(vector<int> arr, int n) {
int temp = 0;
/* 001. A[i-1] < A[i]를 만족하는 가장 큰 i를 찾는다. */
int ii = n - 1;
while (ii > 0 && arr[ii] <= arr[ii - 1]) { ii--; }
/* Last Permutation */
if (ii <= 0) { return false; }
/* 002. A[i-1] < A[j]를 만족하는 가장 큰 j를 찾는다. (j>=i) */
int jj = n - 1;
while (jj >= ii && arr[jj] <= arr[ii - 1]) { jj--; }
/* 003. A[i-1]과 A[j]를 SWAP 한다. */
SWAP(arr[ii - 1], arr[jj], temp);
/* A[ii]부터 순열을 뒤집는다. */
for (int tt = n - 1; ii < tt; tt--, ii++) {
SWAP(arr[ii], arr[tt], temp);
}
return true;
}
#define SWAP(X, Y, Z) Z=X; X=Y; Y=Z;
bool priviousPermutation(vector<int> arr, int n) {
int temp = 0;
int ii = n - 1;
while (ii > 0 && arr[ii] >= arr[ii - 1]) { ii--; }
if (ii <= 0) { return false; }
int jj = n - 1;
while (jj >= ii && arr[jj] >= arr[ii - 1]) { jj--; }
SWAP(arr[ii - 1], arr[jj], temp);
for (int tt = n - 1; ii < tt; tt--, ii++) {
SWAP(arr[ii], arr[tt], temp);
}
return true;
}-
외판원 문제(外販員問題, 영어: traveling salesperson problem) 또는 순회 외판원 문제는 조합 최적화 문제의 일종이다. 줄여서 TSP라고도 쓴다. 이 문제는 NP-난해에 속하며, 흔히 계산 복잡도 이론에서 해를 구하기 어려운 문제의 대표적인 예로 많이 다룬다.
-
여러 도시들이 있고 한 도시에서 다른 도시로 이동하는 비용이 모두 주어졌을 때, 모든 도시들을 단 한 번만 방문하고 원래 시작점으로 돌아오는 최소 비용의 이동 순서를 구하는 것이다.
#include <vector>
#include <climits>
#include <iostream>
#include <algorithm>
using namespace std;
unsigned int generation() {
unsigned static int number = 0;
return number++;
}
int main(void)
{
unsigned int number = 0;
cin >> number;
vector<vector<int> > city = vector<vector<int> >(number);
for (unsigned int ii = 0; ii < number; ii++) {
city[ii] = vector<int>(number);
for (unsigned int jj = 0; jj < number; jj++) {
cin >> city[ii][jj];
}
}
vector<int> visit = vector<int>(number);
generate(visit.begin(), visit.end(), generation);
register int minVal = INT_MAX;
do {
register pair<bool, long> value = make_pair(false, 0);
for (unsigned int ii = 0; ii < number - 1; ii++) {
register int weight = city[visit[ii]][visit[ii + 1]];
if (weight == 0) { value.first = true; continue; }
value.second += weight;
}
/* 도착점에서 다시 출발점으로 돌아오는 경우 (city[ visit[number - 1]][visit[0] ]) */
register int weigth = city[visit[number - 1]][visit[0]];
if (value.first || weigth == 0) { continue; }
if (minVal > weigth + value.second) { minVal = weigth + value.second; }
} while ( next_permutation(visit.begin(), visit.end()) );
cout << minVal << endl;
return 0;
}- 탐욕 알고리즘은 최적해를 구하는 데에 사용되는 근사적인 방법으로, 여러 경우 중 하나를 결정해야 할 때마다 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식으로 진행하여 최종적인 해답에 도달한다. 순간마다 하는 선택은 그 순간에 대해 지역적으로는 최적이지만, 그 선택들을 계속 수집하여 최종적(전역적)인 해답을 만들었다고 해서, 그것이 최적이라는 보장은 없다.
탐욕 알고리즘이 잘 작동하는 문제는 대부분 탐욕스런 선택 조건(greedy choice property)과 최적 부분 구조 조건(optimal substructure)이라는 두 가지 조건이 만족된다. 탐욕스런 선택 조건은 앞의 선택이 이후의 선택에 영향을 주지 않는다는 것이며, 최적 부분 구조 조건은 문제에 대한 최적해가 부분문제에 대해서도 역시 최적해라는 것이다.
이러한 조건이 성립하지 않는 경우에는 탐욕 알고리즘은 최적해를 구하지 못한다. 하지만, 이러한 경우에도 탐욕 알고리즘은 근사 알고리즘으로 사용이 가능할 수 있으며, 대부분의 경우 계산 속도가 빠르기 때문에 실용적으로 사용할 수 있다. 이 경우 역시 어느 정도까지 최적해에 가까운 해를 구할 수 있는지를 보장하려면 엄밀한 증명이 필요하다. 어떤 특별한 구조가 있는 문제에 대해서는 탐욕 알고리즘이 언제나 최적해를 찾아낼 수 있다.
vector<int> coin = {500, 100, 50, 10, 5, 1};
int index = 0;
pair<int, int> answer = make_pair(0, 0);
while (true) {
// 거스름돈의 최적의 해를 구한 경우
if (answer.second == cost) { cout << answer.first << endl; break; }
// 구하고자 한는 값보다 동전의 값이 더 큰 경우는 버린다.
if (cost < coin[index]) { index++; continue; }
// 현재 구해 진 거스름돈에 다음 동전을 더하였을 때 구하고자 하는 값보다 더 큰 경우는 버린다.
if (answer.second + coin[index] > cost) { index++; continue; }
answer.first++;
answer.second += coin[index];
}- 선형 변환에서 회전변환행렬(Rotation matrix)은 임의의 행렬을 원점을 중심으로 회전시킨다. 회전변환행렬(Rotation matrix)은 선형 변환의 성질중 하나이며, 동시에 여러 회전변환행렬중 일부는 대칭변환행렬 즉 반사행렬(Reflection matrix)과 관련이 있다.
/*
* clockwise rotate
* first reverse up to down, then swap the symmetry
* 1 2 3 7 8 9 7 4 1
* 4 5 6 => 4 5 6 => 8 5 2
* 7 8 9 1 2 3 9 6 3
*/
void rotate(vector<vector<int> > &matrix) {
reverse(matrix.begin(), matrix.end());
/*
for (int ii = 0; ii <= length / 2; ii++) {
for (int jj = 0; jj <= length; jj++) { SWAP(matrix[ii][jj], matrix[length - ii][jj], temp); }
}
*/
for (int i = 0; i < matrix.size(); ++i) {
for (int j = i + 1; j < matrix[i].size(); ++j) { swap(matrix[i][j], matrix[j][i]); }
}
}
/*
* anticlockwise rotate
* first reverse left to right, then swap the symmetry
* 1 2 3 3 2 1 3 6 9
* 4 5 6 => 6 5 4 => 2 5 8
* 7 8 9 9 8 7 1 4 7
*/
void anti_rotate(vector<vector<int> > &matrix) {
for (auto vi : matrix) reverse(vi.begin(), vi.end());
for (int i = 0; i < matrix.size(); ++i) {
for (int j = i + 1; j < matrix[i].size(); ++j)
swap(matrix[i][j], matrix[j][i]);
}
}-
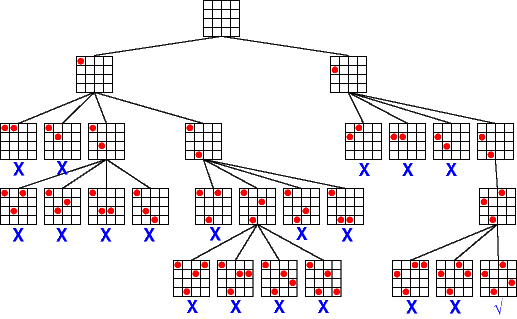
퇴각검색(영어: backtracking, 한국어: 백트래킹)은 한정 조건을 가진 문제를 풀려는 전략이다. "퇴각검색(backtrack)"이란 용어는 1950년대의 미국 수학자 D. H. 레머가 지었다.
문제가 한정 조건을 가진 경우 원소의 순서는 해결 방법과 무관하다. 이런 문제는 변수 집합으로 이뤄지는데, 한정 조건을 구성하려면 각각의 변수들은 값이 있어야 한다. 퇴각검색은 모든 조합을 시도해서 문제의 해를 찾는다. 이것이 장점이 될 수 있는 이유는 퇴각검색 구현 방법들이 많은 부분 조합들을 배제하기 때문이다. 결국 풀이 시간이 단축된다. -
주요 개념은 해를 얻을 때까지 모든 가능성을 시도한다는 점이다. 모든 가능성은 하나의 트리처럼 구성할 수 있으며, 가지 중에 해결책이 있다. 트리를 검사하기 위해 깊이 우선 탐색을 사용한다. 탐색 중에 오답을 만나면 이전 분기점으로 돌아간다. 시도해보지 않은 다른 해결 방법이 있으면 시도한다. 해결 방법이 더 없으면 더 이전의 분기점으로 돌아간다. 모든 트리의 노드를 검사해도 답을 못 찾을 경우, 이 문제의 해결책은 없는 것이다.
퇴각검색은 보통 재귀 함수로 구현된다. 재귀로 파생된 해결 방법은 하나 이상의 변수가 필요한데 , 이것은 현재 시점에서 적용할 수 있는 변수값들을 알고 있다. 퇴각검색은 깊이 우선 탐색과 대략 같으나 기억 공간은 덜 차지한다. 현재의 상태를 보관하고 바꾸는 동안만 차지한다. 탐색 속도를 높이기 위해, 재귀 호출을 하기 전에 시도할 값을 정하고 조건(전진 탐색의 경우)을 벗어난 값을 지우는 알고리즘을 적용할 수 있다. 아니면 그 값을 제외한 다른 값들을 탐색할 수도 있다.
#define HOLE false
#define QUEEN true
#define INT_PAIR pair<int, int>
#define BOOL_VECTOR vector<bool>
#define STRING_VECTOR vector<string>
void fillBoard(vector<BOOL_VECTOR> & board, const INT_PAIR index, const int size) {
const vector<INT_PAIR> direct = {make_pair(0, 1), make_pair(0, -1), make_pair(1, 0), make_pair(-1, 0)
, make_pair(1, 1), make_pair(-1, -1), make_pair(1, -1), make_pair(-1, 1) };
for (int ii = 0; ii < direct.size(); ii++) {
INT_PAIR there = index;
while (true) {
// Case Out Of Range
if (there.first < 0 || there.first >= size || there.second < 0 || there.second >= size) { break; }
// Case Fill
board[there.first][there.second] = true;
there.first += direct[ii].first, there.second += direct[ii].second;
}
}
}
vector<INT_PAIR> findQueenPos(const int size, vector<BOOL_VECTOR> board) {
vector<INT_PAIR> location;
for (int ii = 0; ii < size; ii++) {
for (int jj = 0; jj < size; jj++) {
if (board[ii][jj] == QUEEN) { location.push_back(make_pair(ii, jj)); }
}
}
return location;
}
bool promissing(vector<BOOL_VECTOR> board, const INT_PAIR index, const int size) {
const vector<INT_PAIR> location = findQueenPos(size, board);
for (const auto pos : location) { fillBoard(board, pos, size); }
return board[index.first][index.second]; // TRUE - QUEEN, FALSE - HOLE
}
void backtracking(vector<BOOL_VECTOR> board, const INT_PAIR index, const int size, int depth, int & answer) {
// Case Depth Equal N.
if (depth == size) { answer++; return; }
for (int ii = 0; ii < size; ii++) {
// Case Check Queen Position.
if (promissing(board, make_pair(depth, ii), size) == HOLE) {
board[depth][ii] = QUEEN; // Queen을 놓아 본다.
backtracking(board, make_pair(depth, ii), size, depth + 1, answer);
board[depth][ii] = HOLE; // Queen을 빼본다.
}
}
}- 위상 정렬(topological sorting)은 유향 그래프의 꼭짓점들(vertex)을 변의 방향을 거스르지 않도록 나열하는 것을 의미한다. 위상정렬을 가장 잘 설명해 줄 수 있는 예로 대학의 선수과목(prerequisite) 구조를 예로 들 수 있다. 만약 특정 수강과목에 선수과목이 있다면 그 선수 과목부터 수강해야 하므로, 특정 과목들을 수강해야 할 때 위상 정렬을 통해 올바른 수강 순서를 찾아낼 수 있다. 이와 같이 선후 관계가 정의된 그래프 구조 상에서 선후 관계에 따라 정렬하기 위해 위상 정렬을 이용할 수 있다. 정렬의 순서는 유향 그래프의 구조에 따라 여러 개의 종류가 나올 수 있다. 위상 정렬이 성립하기 위해서는 반드시 그래프의 순환이 존재하지 않아야 한다. 즉, 그래프가 비순환 유향 그래프(directed acyclic graph)여야 한다.
#define INT_VECTOR vector<int>
#define INT_PAIR pair<int, int>
void reculsiveDFS(int index, vector<bool> & visit, vector<INT_VECTOR> & student, vector<int> & answer) {
visit[index] = true;
for (int ii = 0; ii < student[index].size(); ii++) {
const int there = student[index][ii];
if (visit[there] == false) { reculsiveDFS(there, visit, student, answer); }
}
// DFS 종료시 방문 한 정점의 번호를 저장한다.
answer.push_back(index);
}
vector<int> check = vector<int>(input.first);
vector<bool> visit = vector<bool>(input.first);
vector<INT_VECTOR> student = vector<INT_VECTOR>(input.first);
INT_PAIR pos = make_pair(0, 0);
for (int ii = 0; ii < input.second; ii++) {
scanf("%d %d", &pos.first, &pos.second);
student[pos.first - 1].push_back(pos.second - 1);
// 위상정렬의 핵심은 들어오는 간선이 하나도 없는 정점들을 찾아서 결과를 찾는다.
check[pos.second - 1]++;
}
vector<int> answer;
for (int ii = 0; ii < input.first; ii++) {
// 방문하지 않은 정점이며 간선이 존재하는 않은 정점
if (check[ii] == 0 && visit[ii] == false) { reculsiveDFS(ii, visit, student, answer); }
}
// DFS 종료한 뒤 기록된 순서를 뒤집으면 위상 정렬의 결과를 얻는다.
for (auto begin = answer.rbegin(); begin != answer.rend(); begin++) { cout << *begin + 1 << endl; }#define INT_VECTOR vector<int>
#define INT_PAIR pair<int, int>
vector<int> degree = vector<int>(input.first);
vector<INT_VECTOR> adj = vector<INT_VECTOR>(input.first);
for (int ii = 0; ii < input.second; ii++) {
INT_PAIR pos = make_pair(0, 0);
cin >> pos.first >> pos.second;
// 위상정렬의 핵심은 들어오는 간선이 하나도 없는 정점들을 찾아서 결과를 찾는다.
degree[pos.second - 1]++;
adj[pos.first - 1].push_back(pos.second - 1);
}
priority_queue<int> pq;
// 간선이 하나도 존재하지 않는 정점을 우선순위 큐에 넣는다.
for (int ii = 0; ii < degree.size(); ii++) { if (degree[ii] == 0) { pq.push(-ii); } }
// Degree가 0이 되는 것을 Priority Queue에 추가해주며 Queue가 Empty가 될 때 까지 반복한다.
while (!pq.empty()) {
// Priority Queue에서 Pop의 순서가 위상 정렬의 순서가 된다.
const int here = -pq.top(); pq.pop();
cout << here + 1 << " ";
// 현재 Vertax의 Degree를 하나 씩 감소시켜주면서 Degree가 0이 되면 Priority Queue에 저장한다.
for (int ii = 0; ii < adj[here].size(); ii++) {
const int there = adj[here][ii];
degree[there]--; // 현재 Vertax에 연결 된 다음 Vertax의 대한 차수를 하나 감소한다.
if (degree[there] == 0) { pq.push(-there); } // Degree가 0이 되면 Priroirty Queue에 넣는다.
}
}- A Fenwick tree or binary indexed tree is a data structure that can efficiently update elements and calculate prefix sums in a table of numbers. This structure was proposed by Peter Fenwick in 1994 to improve the efficiency of arithmetic coding compression algorithms.
When compared with a flat array of numbers, the Fenwick tree achieves a much better balance between two operations: element update and prefix sum calculation. In a flat array of n numbers, you can either store the elements, or the prefix sums. In the first case, computing prefix sums requires linear time; in the second case, updating the array elements requires linear time (in both cases, the other operation can be performed in constant time). Fenwick trees allow both operations to be performed in O(log n) time. This is achieved by representing the numbers as a tree, where the value of each node is the sum of the numbers in that subtree. The tree structure allows operations to be performed using only O(log n) node accesses.
#define LONG long long
#define INT_PAIR pair<int, int>
/* 가상의 배열 A[]의 부분 합을 빠르게 구현할 수 있도록 한다. 초기화시에는 A[]의 원소가 전부 0이라 생각한다. */
typedef struct FenwickTree {
private:
vector<LONG> tree;
public:
FenwickTree(int n) :tree(n + 1) {}
// A[0..pos]까지의 부분합을 구한다.
const LONG sum(int pos) {
LONG ret = 0;
while (pos > 0) {
ret += tree[pos];
pos -= (pos & -pos); // 다음 구간을 찾기 위하여 최종 비트를 지운다.
}
return ret;
}
// 펜윅 트리 갱신 : A[pos]에 Value를 더한다.
void update(int pos, LONG val) {
while (pos <= this->tree.size()) { this->tree[pos] += val; pos += (pos & -pos); }
}
// A[pos1..pos2]까지의 부분합을 구한다.
const LONG rangeSum(INT_PAIR index) {
return this->sum(index.second) - this->sum(index.first - 1);
}
} FENWICK;
- 어구전철(語句轉綴) 또는 애너그램(anagram)은 단어나 문장을 구성하고 있는 문자의 순서를 바꾸어 다른 단어나 문장을 만드는 놀이이다. 어구전철을 잘 아는 사람들끼리 암호문으로 어구전철을 사용할 수도 있지만 그렇지 못할 경우도 많다. 그 이유는 어구전철은 여러 자의적 해석이 가능하기 때문이다. 예를들어
가나 → 나가, 국왕 → 왕국, 남장 → 장남, 성탄 → 탄성, 순조 → 조순, 비굴 → 굴비, 미개 → 개미, 신발 → 발신, 문전박대 → 대박전문이 있다.
#include <string>
#include <locale>
#include <iostream>
#include <algorithm>
using namespace std;
#define STRING_PAIR pair<string, string>
const bool printAnswer(string first, string second) {
std::sort(first.begin(), first.end());
std::sort(second.begin(), second.end());
return first == second;
}
int main(void)
{
// MARK: - 단어는 알파벳 소문자로만 이루어져 있다.
int number = 0; cin >> number; cin.ignore();
// MARK: - 어구전철(語句轉綴) 또는 애너그램(anagram)은 단어나 문장을 구성하고 있는 문자의 순서를 바꾸어 다른 단어나 문장을 만드는 놀이이다.
// 어구전철을 잘 아는 사람들끼리 암호문으로 어구전철을 사용할 수도 있지만 그렇지 못할 경우도 많다. 그 이유는 어구전철은 여러 자의적 해석이 가능하기 때문이다.
for (int ii = 0; ii < number; ii++) {
STRING_PAIR input = make_pair(string(), string());
cin >> input.first >> input.second;
if (printAnswer(input.first, input.second)) { cout << input.first << " & " << input.second << " are anagrams." << endl; }
else { cout << input.first << " & " << input.second << " are NOT anagrams." << endl; }
}
return 0;
} - LZW(Lempel-Ziv-Welch)는 아브라함 렘펠과 제콥 지브, 테리 웰치가 만든 공통 비손실 데이터 압축 알고리즘이다. 1978년에 렘펠과 지브가 공개한 LZ78 알고리즘의 개선판을 웰치에 의해 1984년에 공개하였다. 이 알고리즘은 빠른 이식을 위해 고안되었지만 데이터의 제한된 분석만 수행하기 때문에 그리 최적으로 동작하지는 않는다. Huffman의 아이디어에서 조금 더 응용된 형태이다.
- 컴퓨터 과학에서, '커누스-모리스-프랫 알고리즘(Knuth–Morris–Pratt algorithm)'은 문자열 중에 특정 패턴을 찾아내는 문자열 검색 알고리즘의 하나이다. 주먹구구식 알고리즘에서 불필요한 문자간 비교를 없애기 위해 Next 데이터라고 하는 패턴 정보를 활용하여 검색 시간을 단축하는 방식이다.
const vector<int> getPartialMatch(const string & first) {
// MARK: - KMP를 통해 자기 자신을 찾는다. N을 N에서 찾는다. begin = 0이면 자기 자신을 찾아버리니 안됨을 주의한다.
int m = first.size(), begin = 1, mached = 0;
vector<int> pi(m, 0);
// MARK: - 비교할 문자가 N의 끝에 도달할 때까지 찾으면서 부분 일치를 모두 기록한다.
while (begin + mached < m) {
if (first[begin + mached] == first[mached]) { ++mached; pi[begin + mached - 1] = mached; }
else {
if (mached == 0) { ++begin; } // 찾고자 한 문자열이 아닌 경우 시작점을 바꾸어 준다.
else { begin += mached - pi[mached - 1]; mached = pi[mached - 1]; }
}
}
return pi;
}
const vector<int> kmpSearch(const string & first, const string & second) {
const int n = first.size(), m = second.size();
vector<int> ret, pi = getPartialMatch(second);
// MARK: - 현재 대응 된 글자의 수의 값을 저장하는 변수
int begin = 0, matched = 0;
while (begin <= n - m) {
// Case 만약 짚더미의 해당 글자가 바늘의 해당 글자와 같은 경우
if (matched < m && first[begin + matched] == second[matched]) {
matched++;
// MARK: - 모든 문자가 찾고자 하는 문자열에 대응 되는 경우
if (matched == m) { ret.push_back(begin); }
}
else {
// MARK: - matched가 0인 경우에는 다음 칸에서 부터 계속한다.
if (matched == 0) { ++begin; }
else {
begin += matched - pi[matched - 1];
// MARK: - begin을 옮겼다고 처음부터 다시 비교할 필요는 없다. 옮긴 후에도 pi[matched - 1]만큼은 항상 일치한다.
matched = pi[matched - 1];
}
}
}
return ret;
}