WGPOT: Wasserstein Distance and Optimal Transport Map of Gaussian Processes

This repository contains a Python implementation of the Wasserstein Distance, Wasserstein Barycenter and Optimal Transport Map of Gaussian Processes. Based on the papers:

• Mallasto, Anton, and Aasa Feragen. "Learning from uncertain curves: The 2-Wasserstein metric for Gaussian processes." Advances in Neural Information Processing Systems. 2017. Matlab Implementation

• Masarotto, Valentina, Victor M. Panaretos, and Yoav Zemel. "Procrustes metrics on covariance operators and optimal transportation of Gaussian processes." Sankhya A 81.1 (2019): 172-213.

• Takatsu, Asuka. "Wasserstein geometry of Gaussian measures." Osaka Journal of Mathematics 48.4 (2011): 1005-1026.

File Description

• wgpot.py contains all functions for computing Wasserstein distance, Barycenter and transport map
• example.py includes several simple examples
• utils.py includes functions for data preprocessing and visualization

Requirement

• Python 3
• Numpy
• scipy

Examples

• Compute the Wasserstein distance between two Gaussian Processes

# Import the function
from wgpot import Wasserstein_GP

gp_0 = (mu_0, k_0)     
gp_1 = (mu_1, k_1)
# mu_0/mu_1 (ndarray (n, 1)) is the mean of one Gaussian Process 
# K_0/K_1 (ndarray (n, n)) is the covariance matrix of one 
# Gaussain Process

wd_gp = Wasserstein_GP(gp_0, gp_1)

• Compute the Barycenter of a set of Gaussian Processes

# Import the functions
from wgpot import GP_W_barycenter, Wasserstein_GP

gp_list = [(gp_0, k_0), (gp_1, k_1), ..., (gp_m, k_m)]  
# gp_list is the list of tuples contains the mean and covariance 
# matrix of one Gaussian Process

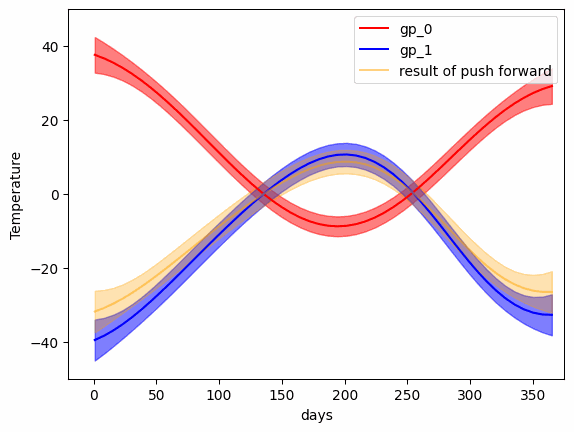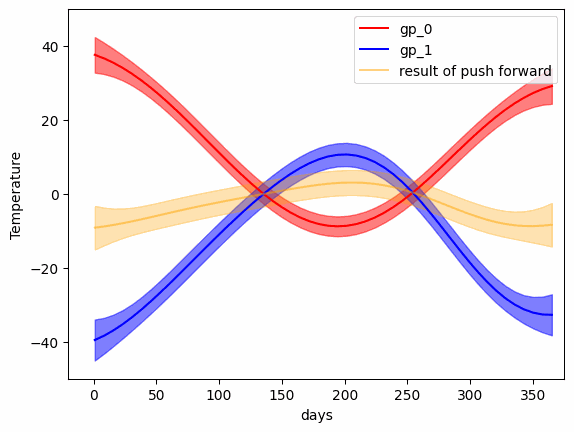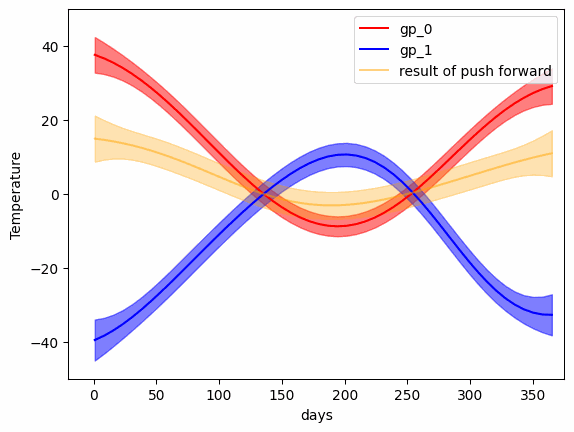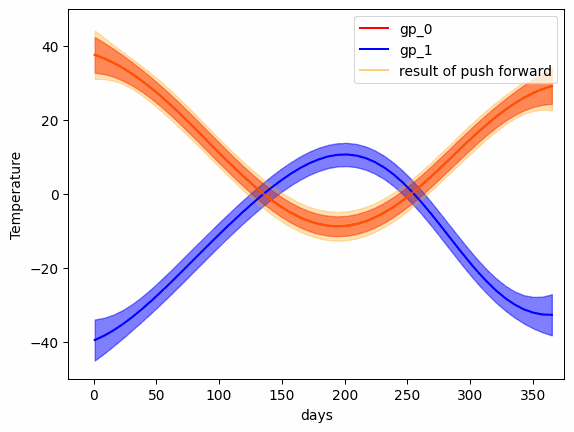
mu_bc, k_bc = GP_W_barycenter(gp_list)

• Transport map (Push forward) from one Gaussian Process to another

from wgpot import expmap

v_mu, v_T = logmap(mu_0, k_0, mu_1, k_1)
# The logarithmic map from Gaussian Distributions on the 
# Riemannian manifold with the Wasseerstein metric

q_mu, q_K = expmap(gp_1_mu, gp_1_K, v_mu_t, v_T_t)
# Exponential map on the Riemannian manifold. For more detials, 
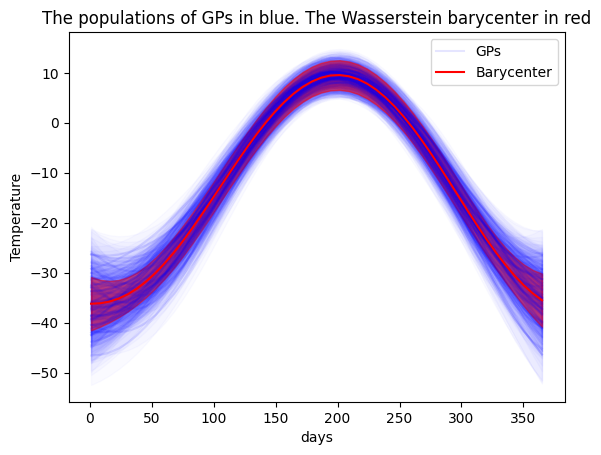
# please refer to [Takatsu, Asuka. 2001]

Results

• The Wasserstein Barycenter between a set of Gaussian Processes

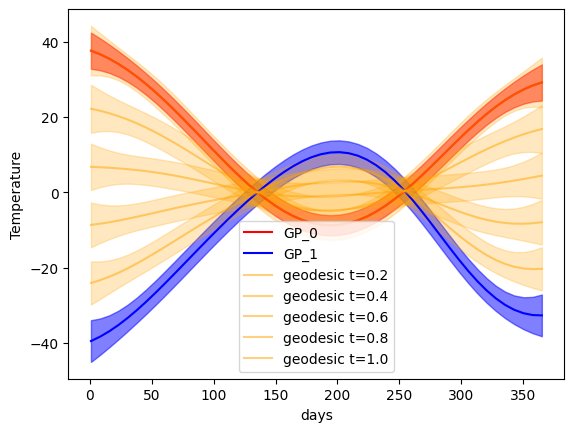
• The transport map (geodesic) between two Gaussian Processes

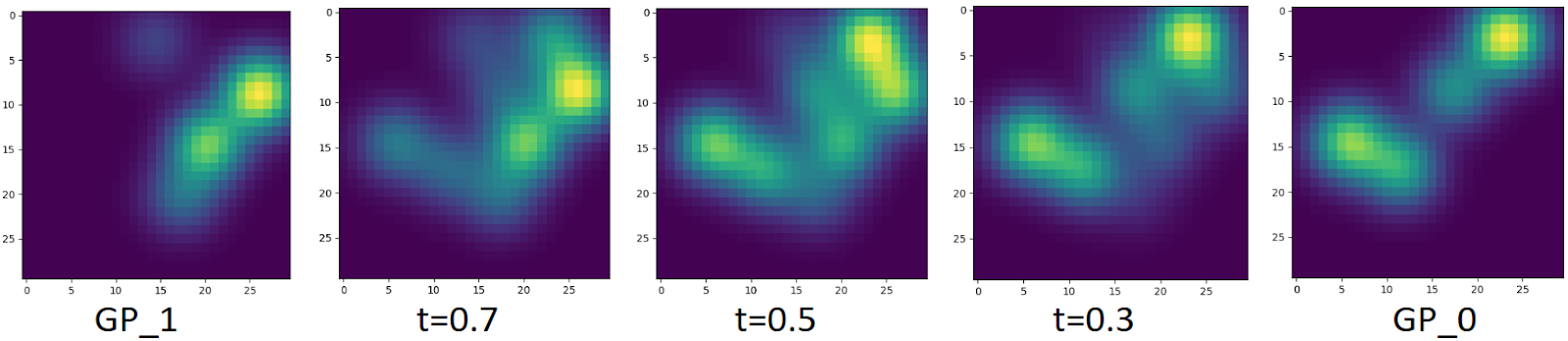
• The transport map between two 2-D Gaussian Processes