# TASK :

Boston Housing DataSet is one of the DataSets available in sklearn. The task is to :

1. Code Gradient Descent for N features and come up with predictions (Market Value of the houses) for the Boston Housing DataSet.
2. Try and test the accuracy with various combinations of Learning Rates and Number of Iterations.
3. Try using Feature Scaling, and see if it helps in getting better results or not.

# UNDERSTANDING THE DATA SET :

⭐ BOSTON HOUSING DATASET :

A DataSet derived from the information collected by the U.S. Census Service concerning housing in the area of Boston Mass.

# GRADIENT DESCENT (A BRIEF INTRO):

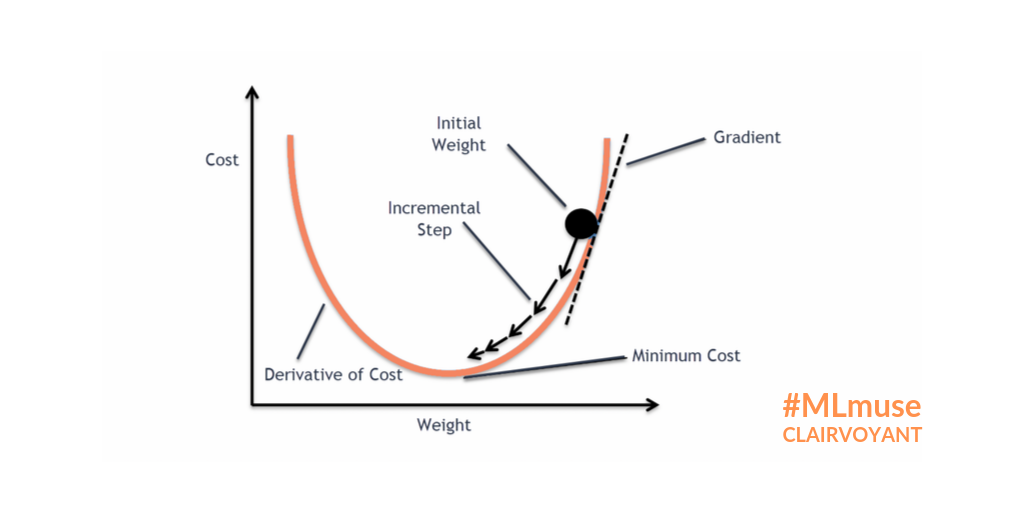
Gradient Descent is an Optimization Algorithm used for minimizing the cost function in various Machine Learning Algorithms. It is basically used for updating the parameters of the learning model.

Types of Gradient Descent :

1. Batch Gradient Descent : This is a type of Gradient Descent which processes all the training examples for each iteration of Gradient Descent. But if the number of training examples is large, then Batch Gradient Descent is computationally very expensive.

2. Stochastic Gradient Descent: This is a type of gradient descent which processes 1 training example per iteration. Hence, the parameters are being updated even after one iteration in which only a single example has been processed. Hence this is quite faster than Batch Gradient Descent.

3. Mini Batch Gradient Descent: This is a type of gradient descent which works faster than both Batch Gradient Descent and Stochastic Gradient Descent. Here b examples where b < m are processed per iteration. If b == m, then Mini Batch Gradient Descent will behave similarly to Batch Gradient Descent.

FORMULAS INVOLVED :

Cost/Error Function = (1/m) Σ( y_i - h(x_i)) ^ 2

θj(jth Coefficient) = θj – (2 * learning rate/m) * Σ( h(x_i)  - y_i) * x_ij , for 1 <= j <= n

where
m is the number of training examples.
n is the number of features.
h(x_i) is the Hypothesis Function for Linear Regression.
Σ is the summation over all the training examples from i = 1 to m.
and x_ij is the jth feature of the ith training data point.