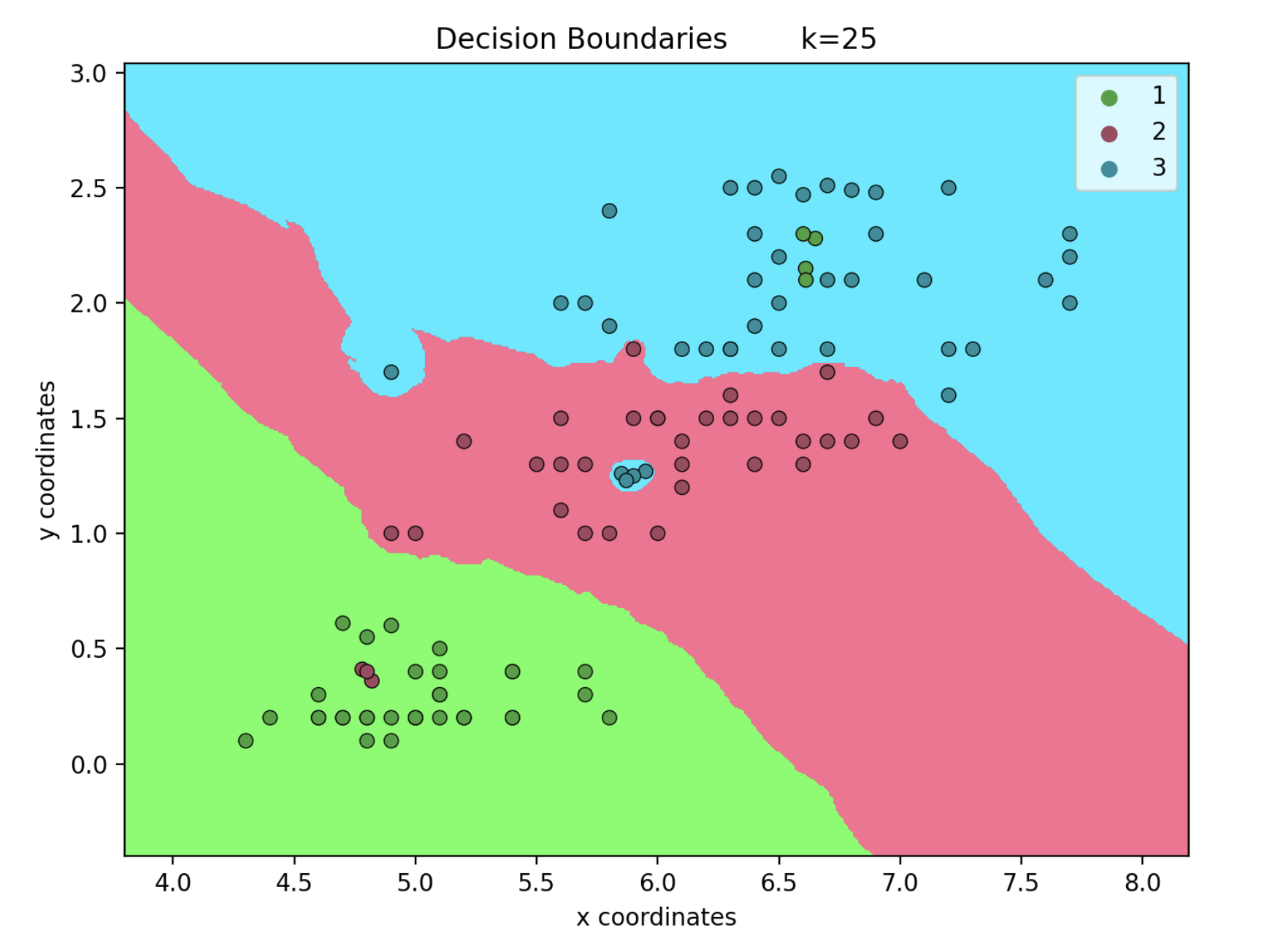
I implemented the k nearest neighbors (kNN) classification algorithm on python. This algorithm is used to predict the classes of new data points using the known data points. We get the coordinates of the new data points and calculate the distances between the new data points and all of the known ones. As the next step, we sort the distances and get ‘k’ number of the closest points. If we were using uniform weights, we would simply count the number of points for each class and the class with the highest number would be our prediction for the new point. However, in this project I used inverse-distance weights, instead of simply counting the points we give weights for each point. These weights are inversely correlated with the distances, so a closer point gets assigned a higher weight.
Additionally, the program compares my kNN algorithm with scikit-learn's algorithm. When the decision boundaries are plotted, we can't see any observable difference between them. You can un-comment the line 164 to test the program with scikit's algorithm.
This algorithm created a problem when the test data and the training data had a point with the same coordinates, because the distance between them would be zero. This would give the point an infinite weight and the other points wouldn’t matter at all. To solve this, I increased the distance to 0.01 whenever the actual distance was zero or lower than 0.01. I decided to use this number because of the dataset that was used. If I have chosen a larger number, there would be lots of points with the same edited distance. If I have chosen a smaller number, points with the same coordinates would get way too heavy weights making it almost the same as the infinite weights problem and this could cause overfitting since an out-of-place point in the training data would influence a significant area in the decision boundary.
When k is 1, we can see that a single or a few points that are outside of their expected region can influence the boundaries a lot. However when k is 25, these outliers have a much less impact on the boundaries. This is because we only take into account the single closest point when k is 1.