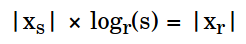Input data are interpreted in different ways and the algorithm is searching for identical parts then. There are two compression methods - it helps to find the best combination (method - parameters of the method - interpretation), which makes data the smallest. After this are computed the most ideal combinations of this combinations to get the most interesting compression ratio - it means, unfortunatelly, when working with huge amount of data, it's needed to have enough computer power. On the contrary, decompression should be really fast and simple process.
Input/output format is Base64. This encoding uses 64 different chars - it means lowercase and uppercase letters of English aphabet (52), numbers (10), the slash sign and the plus sign. We may find there also = chars, to make this string length divisible by 4. The algorithm writes number of equal signs to statistics and they're not compressed - we can consider it to be negligible. The main reason, why I use Base64 encoding is the fact, that 64 chars perfectly fits into a table of 8 rows and 8 columns - it's an easy way, how to get double-digit Oct number.
Because of often transfers between numeral systems is good to make an estimation if it worths. This formula can tell us approximate length after the transfer.
s- a numeral system base of inputr- a numeral system base of output|x|- the length ofx
All values from Base64 fits into a table of 8 columns and 8 rows. The table is here only for an imagination, actually it works converting input chars to it's ASCII codes - check out an example below.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| 0 | A | B | C | D | E | F | G | H |
| 1 | I | J | K | L | M | N | O | P |
| 2 | Q | R | S | T | U | V | W | X |
| 3 | Y | Z | a | b | c | d | e | f |
| 4 | g | h | i | j | k | l | m | n |
| 5 | o | p | q | r | s | t | u | v |
| 6 | w | x | y | z | 0 | 1 | 2 | 3 |
| 7 | 4 | 5 | 6 | 7 | 8 | 9 | + | / |
Here is the example:
var c = a.charCodeAt(pos);
if (countiny_rang(c, 65, 90)) //True means an uppercase letter
{
d = c - 39;
d = transfer(d,10,8); //Converting to the Oct number
}The countiny_rang() function returns true or false, if is c between 65 and 90 (or isn't). The subtraction (d = c - 39;) result transfered to the Oct numeral system gives us the same value as from the table.
It means following:
Input : Hello
Output: 7063545405
Below in this text as "IC". It means n chars in Base64 encoding (i.e. 64^n combinations), which are added where an output string starts and aren't compressed. It serves to save, how both compression methods (described below) were done - it can be considered as summarized statistics about the process. The length of n is changed depending on quantity of informations from the compression. Generally we can mention 2 facts - 1) it's tried to have n in as small length as possible; 2) the longer input the higher value of n (but there's exceptions, naturally).
The input is transfered to the binary system. After it, 0s an 1s are replaced by number of these chars (check out an example below). We're also working with the fact that this string never starts with the zero.
If this number equals something higher then 9, we use lowercase chars of the English alphabet. Although following situation isn't too likely, if is more then 35 one-type chars tohether, first method is cancelled. After it, the algorithm search for the highest char, add 1 to it and the result equals to a new numeral system base. Input is transfered back to the Oct numeral system (these records belongs to IC).
Check out this example:
Input (i.e. x): 37017(8)
Transfer to binary numeral base: x(8) = 11111000001111(2)
Replacing by number of these chars: 554
Transfer back to the Oct numeral base: 554(6) = 326(8)
This string adjustment isn't realized if (ouput.length - x) ≥ 0, naturally. Otherwise, the algorithm assign ouput to x.
It's designed to work with numeral systems in the interval of [9; 36] to. Let's start with the base of 8. At first, the algorithm find out the most frequented pair. It's replaced by 9. This result is transfered back to the Oct numeral system. After it, the length of the "new" string subtracted from the length of the former one. The result of this subtraction is saved with information, that it was the 9-based numeral system and pairs.
It's very similar with trinity, quaternion etc. It depends on the input length how long will be the largest one - it's equals to input/300 (note: I consider this to be too coherent, but creating a better one). Pairs are an exception because they're searched every time. After this the algorithm transfer it to the Oct numeral system and count the difference between the input and ouput lenthts. This stuff is needed to be saved to the IC (with information of the size of the examined group).
Now we have something like a table of the groups and differences. It's chosen and saved only information about the biggest diffrence.
Let me explain how replacing witin numeral systems of bigger bases works. It's almost the same situation as the explained one above, but it's searched for more redundant number groups, which are replaced with chars from the appropriate numeral system.
It means, in a numeral system based with r will be replaced r–8 most common groups using chars out of the Oct one. When done, is the output string transferer back to the numeral system based with 8. This is processed in every numeral system according to the interval above.
Here is an example for the 11-based numeral system and pairs:
Due to the expected severity, algorithm may divide the string to several sub-strings. When this happen, it's needed to write it to the IC.
Let's summarize, what we have in the IC:
- How many times was the first method successful including information about transfering between numeral systems;
- In second method, what combination of lengths of groups in what numeral systems returns (after transfering back to he Oct numeral system) the shortest output - and if this output string isn't longer then the input one.
If are both methods unsuccessful, the algorithm returns the former input with this information.
In another case, we can let out input compressed using the IC data. After it, it's tried to repeat both methods (process of this is mentioned in the IC).
The Dwarferizer isn't ready to use. But don't worry, we are coding as fast as possible.