Python program that models and solves a Rubik's cube using the CFOP method.
(CFOP : Cross, First two layers, Orientation of last layer, Permutation of last layer)
First checkout the notation to understand how rubik's cube notation (aka formulas) work and to understand the output.
To understand the code or to write your own version, read the brief explanation given below.
The code for cube manipulation can be found in cube.py.
The parsing, condenstion and validation for formulas can be found in helper.py.
You can create a cube object and move it by using the following code
from cube import Cube
cb = Cube()
cb.doMoves("RUR'U'")
# to automatically scramble the cube, use
from helper import getScramble
cb.doMoves(getScramble(10))
print(cb)The code for solving the cube can be found in solver.py and its helper data objects in solver_data.py.
If you want to use the solver, add the following code
from solver import Solver
solver = Solver(cb)
solver.solveCube()
# to optimize move count (by removing perspective move redundancy), use
solver.solveCube(optimize=True)
moves = solver.getMoves()
# or for more detailed, decorated and condensed output
moves = solver.getMoves(decorated=True)
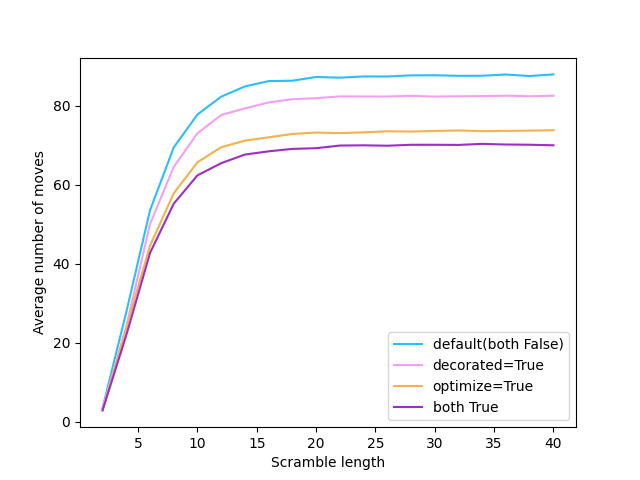
print(moves)The following table shows the average number of moves (each taken over 10,000 solves) it takes to solve the cube for different parameters, each calculated for a different scramble length.
Average number of moves:
| scramble length | default (with both False) | with decorated=True | with optimize=True | with both True |
|---|---|---|---|---|
| 5 | 41 | 38 | 35 | 32 |
| 10 | 78 | 73 | 66 | 62 |
| 20 | 87 | 82 | 73 | 69 |
There are rules and methods that need to be followed in order to use the program.
- The moves in a rubik's cube are defines as follows, (Note: The picture shows the front face as Blue, but the code uses Green as the front face. But the idea remains the same)
If you make the move anticlockwise (opposite to what has been shown in the image) then you "'" or "P" to the move.
R in anticlockwise (opposite to image depiction) direction becomes R'. - The cube printing format is defined as
YYY YYY YYY RRR GGG OOO BBB RRR GGG OOO BBB RRR GGG OOO BBB WWW WWW WWW - The cube index format (if you want to tinker with the code) is defined as
5 3012 4 - The cube front face is assumed as Green and the top face is assumed as Yellow (If input is given otherwise, it automatically reorients itself)
- The cube face notation followed in this code,
Creating this algorithm is not as hard as it sounds, but rather time taking and laborious. The entire task is of reducing cases and applying the appropriate formulas for those cases. If you know how to solve a cube, you should be able to follow my explanation.
-
The first part is to solve the white cross. This has no straight forward formulas to do it and is rather very intuitive. But for a program to solve it, we need to give explicit instructions. This is a major challenge as we need to figure out patterns in a place where intuition is required.
One way to solve this is using 2 state algorithm where we convert all possible cases into a set of standard cases. Then for each of these standard cases we need can apply the corresponding formula. But doing this way is very inefficient as the average number of moves to solve the cross is around 25.
Due to this, i needed to come up with a clever technique to tackle the inefficiency. One major upgrade is the changing of perspectives from global to local. This will save us a ton of code and will reduce the cases. The other is flexible base orientation, where we do not first fix the edge alignment but rather give importance to edge orientation. Depending on the best orientation and the corresponding slot available, we can use a predefined set of formulas to orient the edges and in the end align the edges. This method reduces the average number of moves to solve the cross to around 10.
-
The second part is to solve the first layer simulatenously along with the second layer, and hence is called the F2L (first two layers). This way of solving the two layers is complicated and requires a lot of intuition. One easy work around is to simply use the beginners method where we solve the two layers individually and the whole process is algorithmic. Hence it is much easier to code (with an added bonus that it has only 3 formulas to code up). But as you might have guessed, it is rather inefficient.
So to reduce the number of steps, we use the concept of F2L. If we break down all the possible combinations with color variability, it turns out there are only 41 cases. In a real solve, we do not remember all the cases but rather intuitively reduce most cases to easily solvable ones. But if we do want, there are formulas for each of these cases. So, rather than intuition we can now use the formulas for each of these cases. Now the task is pattern recognition, meaning how to determine which formula to apply (given it is color variable). The simple method is to find some kind of orientation dependant hash and then compare the hashes to get the formula. Another challenge is the wide variety of cases and scenarios present. Once we figure out hashes for the many scenarios present, then its pretty straight forward to apply. The last problem is to fix non standard cases. I tackled this by using a scoring system, where the moves (to convert non standard to standard) which are shorter and pair up corner-edge are given more score. Read this document for the F2L cases and scenarios.
-
The third step is orientation of the last layer (OLL). At this point it is very straight forward and easy but labour intensive. The actual code to implement this takes 5 minutes but to write down formulas for each of the cases (and make it into a dictionary) takes a lot of time. Simply put, we convert the orientation of yellow positions on the top layer into a hash string and use that to look up in the oll dictionary that we made by hashing the standard cases similarly. Thats it!. Read this document for the OLL cases.
-
The fourth and final step is permutation of the last layer (PLL). This step is very similar to the previous step. I used a color independant orientation based technique to identify the cases. My method is brute force (to enable color independence) rather than implementing a color independent hash. Since the compare cases are few, this wont affect the speed much. Read this document for the PLL cases.