Node2Vec on DBLP Citation Graph

About DBLP Citation Graph

The DBLP Citation graph contains papers as the nodes and the references made as an edge to the other paper nodes. In addition to this there are features for each paper like venue, keywords, field of study, etc. Using Node2Vec algorithm, the feature embeddings are retireved for the task of spectral clustering. For our problem we choose DBLP dataset, created by the Database Systems and Logic Programming research group at the University of Trier, Germany, contains information about various research papers, conferences and authors.

Whole dataset as citation graph:
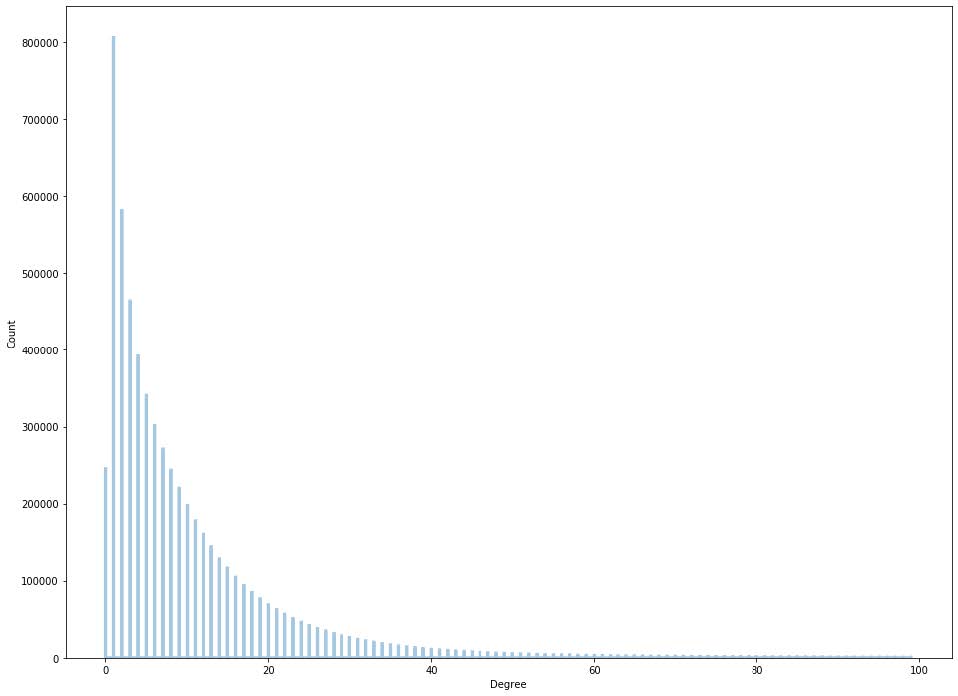
Number of nodes: 6703290
Number of edges: 375344782
Average degree: 12.1303
Number of Distinctly connected Components: 269609

Some connected components of the Citation graph:

Degree Distribution of the Citation Network (degree vs count of nodes):

Node2Vec

Graph Networks have been used as a medium for representing data and the relationships between the data and the database. It provides a data structure equipped to model the real world data and visualize it in a form that is innate to human understanding. It represents relationships as connections and objects as nodes, and there are standard techniques that have been built to describe graphs. We establish the concept of sensemaking in graphs as tasks involving prediction of the labels, and link prediction between two nodes of a given graph network. For predicting labels or classifying a node, we cluster a node with other nodes that have higher probability of having the same label. Some applications of classification task on graph network are predicting functional labels of proteins in a protein - protein interaction graph, and predicting political affiliations based on purchase history. Link prediction task can be used in recommendation systems and predicting real world friends. In this graph, each paper is represented as a node where an edge between nodes exists if a paper cites another paper. The network is sparse, proving to be both an advantage, to design discrete algorithms given the task at hand, and a disadvantage, harder to generalize sparse data for statistical learning. Any supervised learning will require a set of discriminating and informative domain specific features based on expert knowledge, which becomes harder for such graphical representations.

We have used the node2vec algorithmic framework in order to learn continuous feature representations from our input graph. This is a step that facilitates a number of downstream machine learning tasks. In our specific case, we have used it to aid the Skip-Gram algorithm, where the optimization problem can be modeled as:

where, is the likelihood of observing a node that lies in the neighborhood of node u and f is the d dimensional mapping of the graph to feature representation we are trying to learn. For every node u, which is the set of all vertices (nodes) present in the graph. This relationship of being neighborhood of a node is assumed to be independent of all other nodes and its effect on the presence of this relationship.
To smoothly interpolate between DFS and BFS search algorithms for creating neighborhood for a node, the framework defines a biased random walk algorithm using DFS and BFS both. A fixed length random walk is generated from transition probabilities as:

The equation defines conditional probability for reaching node c (on ith step) from node v (i-1th step), using the transition probability and normalizing constant Z. For every node pair the transition probability is defined on the basis of parameters p and q to guide the search function . Shortest distance between given nodes d, and parameters p (probability of immediately revisiting a node) and q (degree of exploration) is used to set this search bias function,

Spectral Clustering

After our network is aptly converted into nxd dimensional feature matrix from the skip gram, there are two tasks that can be performed. For performing clustering task, we perform eigen decomposition for finding eigen-vectors corresponding to k smallest eigen-values. Spectral Clustering is performed for dimension reduction followed by K-Means, creating k partitions in the graph based on some similarity metric. The clustering is optimized by minimizing the following objective function,

where L is the Laplacian matrix, H is the eigen-vector of the sparse laplacian matrix, and I is the identity matrix. As mentioned, the laplacian matrix of the citation network is very sparse, and calculating an inverse of L is very costly. Scipy.sparse uses ARPACK algorithm to efficiently pick second smallest eigen-value directly using linalg.eigsh even when the input matrix is sparse.

Citation Graph Clustering Result

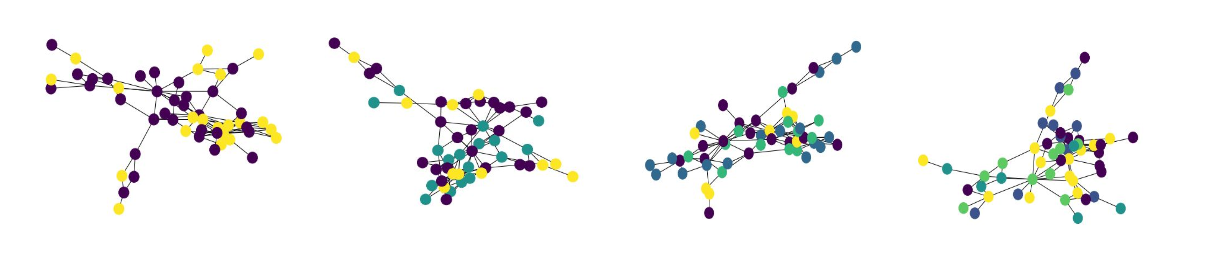
Given below are results of spectral clustering for k=2 to k=5:

References

1. Schloss Dagstuhl Leibniz Center for Informatics. Dblp.org,May 2020.
2. Loredana M. Genovese, Marco M. Mosca, Marco Pellegrini,and Filippo Geraci. Dot2dot: accurate whole-genome tan-dem repeats discovery.Bioinformatics (Oxford, England),35(6):914–922, Mar 2019. 30165507[pmid].
3. Aditya Grover and Jure Leskovec. node2vec: Scalable fea-ture learning for networks.CoRR, abs/1607.00653, 2016.
4. Peter Hoff, Adrian Raftery, and Mark Handcock. Latentspace approaches to social network analysis.Journal of theAmerican Statistical Association, 97:1090–1098, 02 5. Akihiro Inokuchi, Takashi Washio, and Hiroshi Motoda.Complete mining of frequent patterns from graphs: Mininggraph data.Machine Learning, 50(3):321–354, Mar 2003.
5. Yu Jin and Joseph F. J ́aJ ́a. A high performance implemen-tation of spectral clustering on CPU-GPU platforms.CoRR,abs/1802.04450, 2018.
6. David Liben-Nowell and Jon Kleinberg. The link predictionproblem for social networks. InProceedings of the TwelfthInternational Conference on Information and KnowledgeManagement, CIKM ’03, page 556–559, New York, NY,USA, 2003. Association for Computing Machinery.
7. Maschhoff, , K. J. Maschhoff, K. J. Maschhoff, D. C.Sorensen, and D. C. Sorensen.P arpack: An efficientportable large scale eigenvalue package for distributed mem-ory parallel architectures.
8. Tomas Mikolov, Kai Chen, G.s Corrado, and Jeffrey Dean.Efficient estimation of word representations in vector space.Proceedings of Workshop at ICLR, 2013, 01 2013.