-
Notifications
You must be signed in to change notification settings - Fork 237
Dynamic
The following illustrates the library decomposition into components and their functions. The structure is depicted in the following figure.

The library components are categorized by execution time: tune-time or run-time components. The tune-time components are the 'analyzing tools' and 'kernel generators', while the 'solving strategy selector' and 'OpenCL solver' are runtime components. However, the generators can be used during runtime too if kernel building is done on the fly. 'Analyzing tools' will run a set of tests to determine hardware features, find optimal solution paths for different problem sizes and to estimate performance of kernel sequence calls. After tuning, it writes obtained results to the 'kernel and preferences storage'. This storage has a separate file per each device found in the system. Kernel generators produce kernels for different types and subproblem sizes. 'Solution selector' gets the most appropriate solution pattern and subproblem sizes based on the input matrix sizes. The 'OpenCL solver' is the core component which performs computations and returns solution to the host. 'Kernel and preferences storage' contains generated optimal kernels and preferred problem sizes for different solution patterns that are used during runtime by the 'solution selector'.
Global shared memory is the major bottle-neck in any multicore or multiprocessor system. Therefore, the primary effort of the library is to create effective memory access patterns. The 'memory access pattern' refers to a set of levels in the hardware's hierarchical memory model and the memory access order affecting the performance degradation related to these levels. The patterns discussed below assumes that both matrices are divided into panels which are then distributed among compute units and thread processors. The amount of memory transfers related to the output matrix won't vary for different patterns; it doesn't make considerable contribution to the total algorithm cost, and were not taken into account for simplicity. It's assumed that matrices can be greater than any given cache level, and all algorithm considerations are done for the generic case. It's implied that the same memory patterns are used not obligatory for generic rectangular matrices, but for more specific matrices too and we restrict ourselves to the case of generic rectangular matrices.
As it is shown in the figure below, both matrices are divided into blocks which are consecutively copied to local memory and take part in block multiplication. Block heights are named M and N. Depending on the problem, every panel of the B matrix or a panel pair is assigned to a dedicated compute unit. Each respective block are then multiplied by all the compute unit's thread processors in parallel. Block sizes are chosen with the following restriction: the matrix A, B and C blocks combined should not exceed the size of the local memory of the compute unit. The algorithm cost in the worst case can be expressed by the following formula
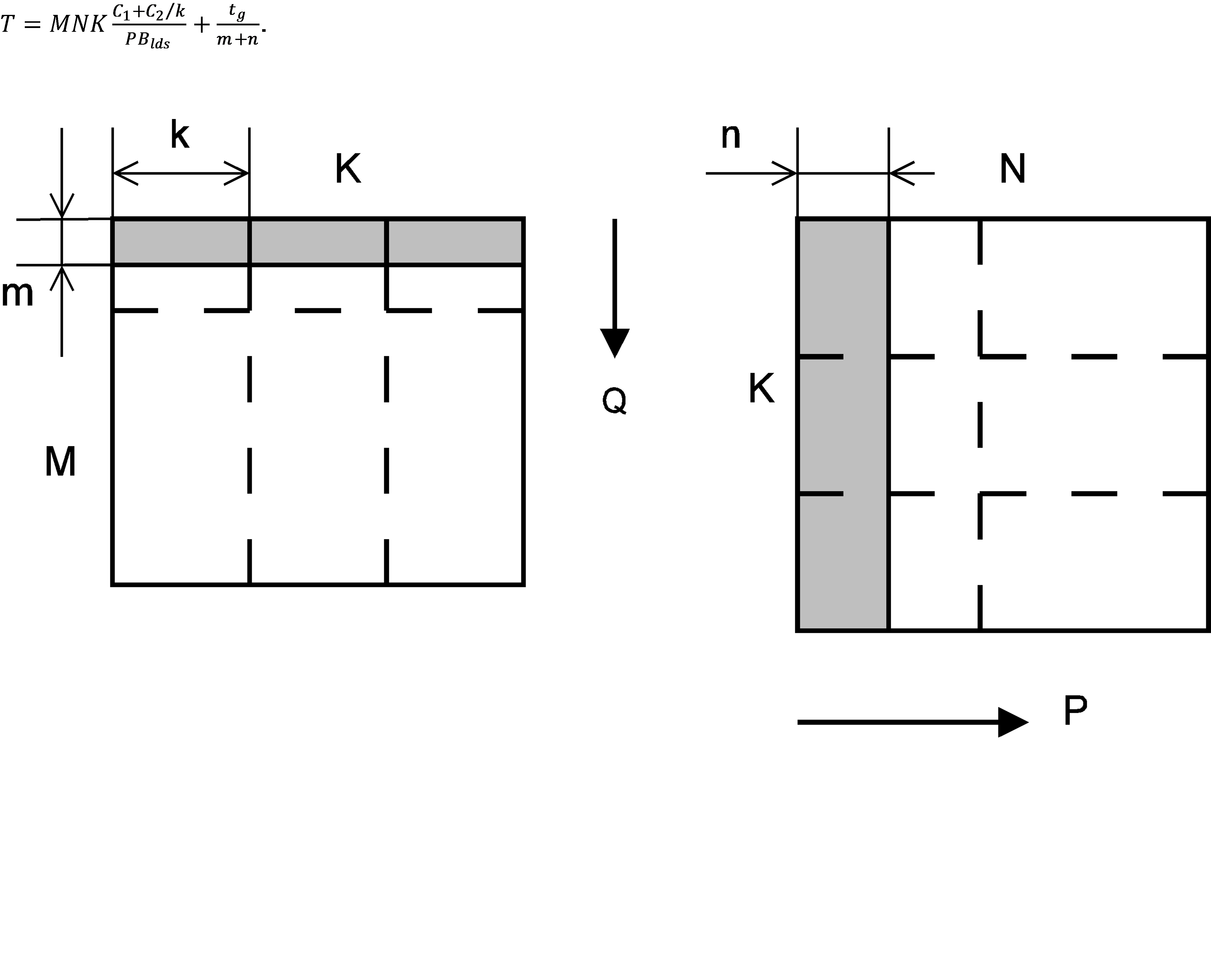 with
with
- P - number of compute units,
- B_lds - number of local memory banks
- t_g - access cost for the global memory bypassing the cache subsystem
The general approach is the same as the previous LDS section description except that one or both matrices are preliminary copied to an image object; the goal is to leverage fast texture cache. Block sizes are chosen such that they fit in the L1 cache. When both matrices are stored to an image, the blocks became confluent in the sense that each tile product can be evaluated continuously over the whole K.
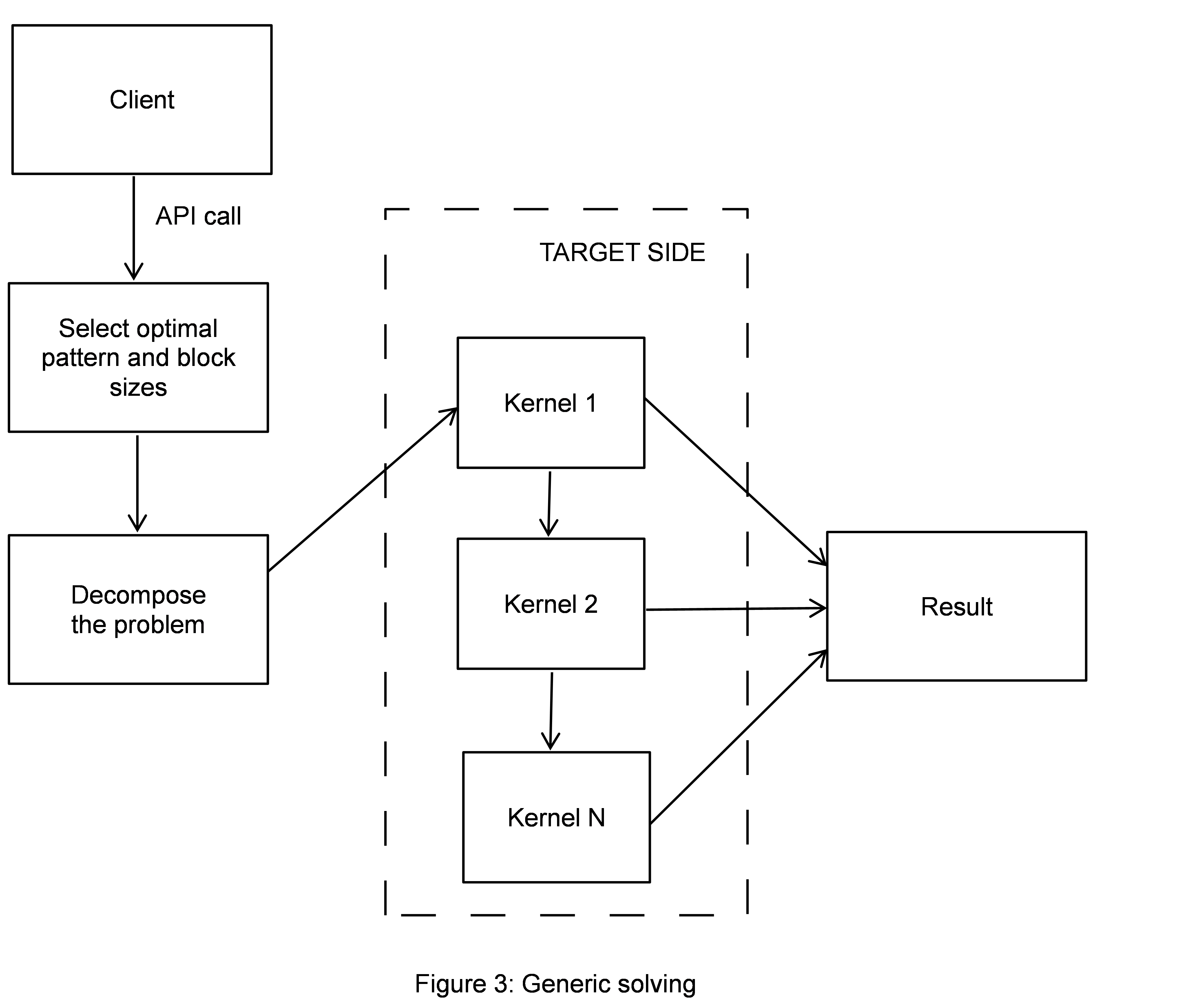
This is done in runtime to choose an optimal solution for the given problem parameters. To carry out this task, it uses statistics collected at the tune time. The figure below depicts the solving process in general. First, the strategy selector retrieves the best memory pattern realized in an OpenCL kernel with optimal block sizes. The component decomposes the problem into a set of non-intersecting subproblems. Typically, this is done to process tails separately for higher efficiency, or when an image buffer sizes is insufficient to evaluate the problem in single step, or to distribute the problem between several devices. All kernels are executed strictly in-order to avoid unexpected side effects involving performance or correctness.
A product of a triangular matrix by a rectangular one is evaluated the same way as with GEMM, but the leading or trailing zeros in the panels of the triangular matrix are skipped at multiplications.
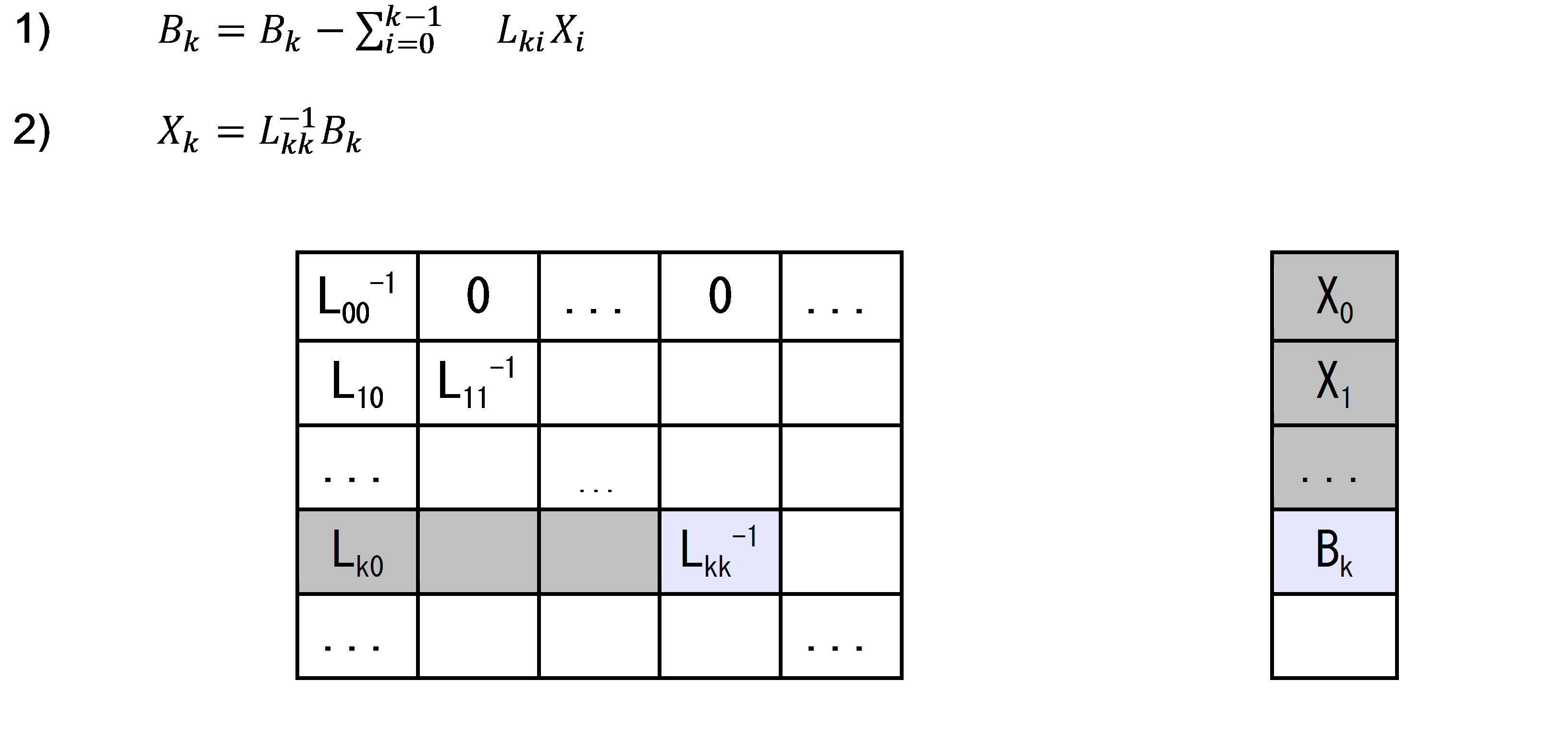
For linear equation systems solving, a block algorithm is used. LX=B, where L is lower triangular matrix M×M, X and B are rectangular matrices M×N. Columns of matrix B are divided into panels with fixed width n; each panel is processed on one compute unit. Matrix L is divided into square blocks with fixed size M. Diagonal blocks L_ii are pre-inverted. After the inversion, all nonzero blocks are placed into memory sequentially. The final matrix rearrangement:
 With this matrix representation, a solution can be obtained with the sequential arrangement of the L blocks.
With this matrix representation, a solution can be obtained with the sequential arrangement of the L blocks.
 Total number of arithmetical operations is MN((M+m))⁄2, which are separated between PQ processors. Total cost of memory access for matrix B is proportional to MN((M+m))⁄2n. Total cost of access to matrix A blocks is proportional to MN((M+m))⁄2m.
Total number of arithmetical operations is MN((M+m))⁄2, which are separated between PQ processors. Total cost of memory access for matrix B is proportional to MN((M+m))⁄2n. Total cost of access to matrix A blocks is proportional to MN((M+m))⁄2m.
Basically, every BLAS generator consists of the following steps:
- Initialize generator settings
- Create generator context
- Declare kernel and needed local variables
- Generate a tile multiplication loop for the integrally divisible problem part
- Generate a tile multiplication for tails
- Generate updating result stored in the global memory
- Destroy generator context
The steps 4 and 5 are typically done with leveraging of the tilemul generator: tileMulGen() and
genMulTiles(). The step 6 is typically done with the updateResultGen() generator.
At the time of kernel execution, threads typically operate with small matrix pieces. They are named "tiles" and every tile is guaranteed to not intersect with others. The set of all tiles with which a kernel works in a given run consists of the useful part of the matrix. The generator API presents a 'Tile' structure. Every tile is stored in the thread's private area in either the form of an array or a set of variables. It can be stored in direct or transposed form. An API is provided to initialize, declare storage and generate useful primitive operations in an easy way.
A tail is a trailing part of an input or output matrix which is smaller than a single block. There are 2 type of tails: top and bottom level. A matrix has a top level tail if
either matrix size is not integrally divisible by the size of blocks processed cooperatively by a single work group. Likewise, low level tails relate to blocks processed by a single work
item (tiles). The front-end notifies generators about the presence of tails with the following flags: KEXTRA_TAILS_Y_TOP, KEXTRA_TAILS_X_TOP, KEXTRA_TAILS_BW_TOP, and KEXTRA_TAILS_Y_BOTTOM, KEXTRA_TAILS_X_BOTTOM, KEXTRA_TAILS_BW_BOTTOM which are all members of the KernelExtraFlags enumeration.
The presence of tails impacts tile fetching and generators should take care to not exceed buffers by means of selecting an addressing mode when invoking the fetch subgenerator and
zeroing the tails after fetch. A defaultTilePostFetch() function is provided which generates zeroing code. It is supposed to be used in most cases as a postfetch callback passed to the tilemul generator tileMulGen().
The Kernel Generator infrastructure provides essential assistance in generating kernel source. The main goal is to relieve generators from concerns on code formatting, source length evaluation and name conflicts for functions and variables.
The generator context is an object representing the generator state at a specific moment of time.
It incorporates information about all declared function and variables, current nesting depth
and available space in the source buffer. A new context is created with createKgenContext()
and destroyed with destroyKgenContext(). A context may be reset to the initial state with
resetKgenContext(). The last feature is useful if a temporary context is needed to
generate a few small pieces of code.
An inline code section is a piece of a generated function having its own code management context.
Such a context has a list of variables associated with it and its own policy and set of statements
to be reordered. There are 2 functions with which any part code produced by a generator can be
enclosed in the inline section. These are kgenStartInlineCode() and kgenEndInlineCode(). Any inline
code section is associated with a subgenerator or a main kernel generator. There may be only one
associated subgenerator and the sections can be nested. After beginning the body of a function the
context starts the default inline section, thus, there is no need to enclose the whole function
body in the section explicitly.
Basically, all implementations of the BLAS functions should consist of a series of typical steps.
For example, matrix block multiplication is one such step. There may be a lot of the others concerning hardware optimization, such as loading preliminary elements
into registers, writing given result back and so on. As a result, the idea to develop dedicated subgenerators looked quite natural. On the other hand, pieces of code
produced by such subgenerators may need to save states or need to be organized in the proceduring
way. In order to make subgenerators usable and flexible there needs to be special mechanisms
allowing them to enclose needed code parts in dedicated functions while they are currently not at
the global scope, and to select scope for its auxiliary variables.
This allows to fully incapsulate any subgenerator specifics and free the main generators
from auxiliary logic before/after invoking the subgenerators. For most cases of using code
management features, code generation should be expected to be completed in 2 passes. The common scenario
is the following: code is first placed in a context shadow buffer and flushed at context destroy or kgenFlush() invocation. In a few cases,
the code could be stored to the main buffer right away.
Subgenerators take care of declaring of all local variables they might encounter, given 2 possible issues: name conflicts and performance penalties. Since 2 different subgenerators don't know and shouldn't know anything about the specifics of each other, situation like the following might occur: generator A declares a variable of type X, and generator B declares a variable of type Y and they both have the same name; if the code produced is within the same scope, obviously a compilation error occurs. Enclosing the generated code to a dedicated scope is a possible solution, but this dirties the source with unrelevant syntactic items making it harder to read. Another point is that this solution basically doesn't avoid declaration of unneeded items. Next problem, the generated code may be executed in a loop. Moreover, it may be generated in little pieces. Hence, if the declaration includes initialization code, it may have significant impact on performance. A possible solution to avoid such impact could be an external declaration, initialization, modification and passing variable names to the subgenerator. However, this leads inevitably to a stodgy interface and requires auxiliary functions for every such subgenerator to declare/initialize/modify the needed variables.
To facilitate the situation, the kernel infrastructure provides for the watching of variables.
It provides automated scoping in the case of name conflicts and reusing variables allowed to be
shared among different code pieces. New variables are added to the generator context with the
kgenDeclareVariables() function. Every variable lives within an inline code section, and
if that piece of code in which a variable is declared is not enclosed in a section explicitly,
the variable lives in the default inline section covering the whole function body. A variable
may be private for the generator owning the current inline section or can be shared among different
subgenerators. The variable sharing policy is regulated with the flags that are a part of the KvarDeclFlags
enumeration. Basically, there are 2 sharing policies; the first one allows sharing only among non-nested inline sections,
and the second one does allow sharing among the nested sections. The 2 policies can be
combined, and the variable can be shared among nested and not nested sections. While declaration
scope is not restricted by the current scope, the declaration in backward scopes should be used in
very limited cases since it reduces the transparency of code generation and can bring lots of
confusion.
Any variable declarations bypassing this feature may lead to unresolved name conflicts and thus should be avoided within the kernel body.
Let's consider some examples.
Example 1. Let's have 2 subgenerators producing code in different inline sections, declaring an auxiliary variable used for example for saving precomputed offset in global memory. Let the first subgenerator to contain the following code:
kgenDeclareVariables(ctx, SUBGEN_ID_1, "uint off = m * lda + k;\n", KVAR_SHARED_NOT_NESTED, 0);
kgenAddStmt(ctx, "a = A[off];\n");Let the second subgenerator contain the following code:
kgenDeclareVariables(ctx, SUBGEN_ID_2, "uint off = m * ldc + n;\n", KVAR_SHARED_NOT_NESTED, 0);
kgenAddStmt(ctx, "C[off] = c;\n");Called sequentially, they produce the following OpenCL code:
uint off = m * lda + k;
a = A[off];
...
off = m * ldc + n;
C[off] = c;Example 2.
Let's consider the same situation, but the second subgenerator doesn't want to
share its variable and doesn't specifiesKVAR_SHARED_NOT_NESTED flag at calling
kgenDeclareVariables(). The produced code is as follow:
uint off = m * lda + k;
a = A[off];
...
{
uint off = m * ldc + n;
C[off] = c;
}Example 3. A main generator produces a loop and invokes a subgenerator notifying it that generated code is in the loop body. The subgenerator brings variable declaration out of the loop. A piece of code in the main generator
kgenBeginBranch(ctx, "for (i = 0; i < endi; i++)");
subgen(ctx, ...);
kgenEndBranch(ctx, NULL);A piece of code in the subgenerator
kgenDeclareVariables(ctx, "uint4 off = {0, lda, lda*2, lda*3};\n", KVAR_SHARED_NOT_NESTED, -1);
kgenAddStmt(ctx, "a0 = A[off.x];\n"
"a1 = A[off.y];\n"
"a2 = A[off.z];\n"
"a3 = A[off.w];\n"
"off = off + 1;\n");
...The respective generated OpenCL code is
uint4 off = {0, lda, lda*2, lda*3};
for (i = 0; i < endi; i++) {
a0 = A[off.x];
a1 = A[off.y];
a2 = A[off.z];
a3 = A[off.w];
off = off + 1;
...
}AMD GPUs don't support memory operands in arithmetic instructions; operands are explicitly loaded from memory into registers. In the same way, if a result needs to be stored to memory, it is done with dedicated instructions. In addition, the same kind of instructions are grouped into clauses. Switches between different clauses causes pipeline latencies. Thus, good optimizations assume explicitly grouping the same kind of statements within the OpenCL kernel code. However, implementing this optimization in generators can complicate their implementations. Even worse, it is a significant impact on generator modularity. Subgenerators have to deal with global memory performing arithmetic operations at the same time and can be invoked multiple times and produce code in little pieces. This will in turn lead to multiple clauses with little amounts of work in each and significant overhead.
In order to help to resolve these problems, the infrastracture offers statements reordering.
The reordering is done within a single inline section or between clustered sections produced by the
same subgenerator. A caller is able to select which policy of reordering should be applied
in a particular section. It is selected at section beginning and remains in effect untill the end of the
section. Supported policies are enumerated with the KgenReorderPolicy enumeration. In a basic case,
a user is free to disable any actual reordering using the KGEN_POLICY_DIRECT policy.
Example.
Let's consider the following code generating square-low block summation for data
stored in global memory, leveraging a function generating this operation for a single
element.
void genGmemSquareSum(
struct KgenContext *ctx,
const char *type,
const char *dst,
const char *src)
{
static int i = 0;
char buf[1024], tmpSrc[64], char tmpDst[64];
kgenStartInlineCode(ctx, SUBGEN_ID, KGEN_RPOLICY_MERGE_FAS);
kgenDeclareVariables(ctx, "%s tmp0, tmp1, tmp2, tmp3, tmp4, tmp5, tmp6, tmp7;\n\n",
KVAR_SHARED_NOT_NESTED, 0);
sprintf(buf, "tmp%d = %s;\n"
"tmp%d = %s;\n",
i, src, i + 4, dst);
kgenAddTypifiedStmt(ctx, buf, STMT_TYPE_FETCH, 0, false);
sprintf(buf, "tmp%d = mad(tmp%d, tmp%d, 0);\n"
"tmp%d = mad(tmp%d, tmp%d, tmp%d);\n",
i, i, i, i + 4, i + 4, i + 4, i);
kgenAddTypifiedStmt(ctx, buf, STMT_TYPE_ARITHM, 0, false);
sprintf(buf, "%s = tmp%d;\n", dst, i + 4);
kgenAddTypifiedStmt(ctx, buf, STMT_TYPE_STORE, 0, false);
kgenEndInlineCode(ctx);
i = (i + 1) % 4;
if (i == 0) {
kgenFlush(ctx, false);
kgenAddBlankLine(ctx);
}
}
kgenAddStmt(ctx, "uint8 ca = {0, lda, lda*2, lda*3, lda*4, lda*5, lda*6, lda*7};\n"
"uint8 cb = {0, ldb, ldb*2, ldb*3, ldb*4, ldb*5, ldb*6, ldb*7};\n\n");
for (int i = 0; i < 8; i++) {
char src[64], dst[64];
sprintf(src, "A[ca.s%d]", i);
sprintf(dst, "B[cb.s%d]", i);
genGmemSquareSum(ctx, "float4", dst, src);
}This will producing the following OpenCL code:
uint8 ca = {0, lda, lda*2, lda*3, lda*4, lda*5, lda*6, lda*7};
uint8 cb = {0, ldb, ldb*2, ldb*3, ldb*4, ldb*5, ldb*6, ldb*7};
float4 tmp0, tmp1, tmp2, tmp3, tmp4, tmp5, tmp6, tmp7;
tmp0 = A[ca.s0];
tmp4 = B[cb.s0];
tmp1 = A[ca.s1];
tmp5 = B[cb.s1];
tmp2 = A[ca.s2];
tmp6 = B[cb.s2];
tmp3 = A[ca.s3];
tmp7 = B[cb.s3];
tmp0 = mad(tmp0, tmp0, 0);
tmp4 = mad(tmp4, tmp4, tmp0);
tmp1 = mad(tmp1, tmp1, 0);
tmp5 = mad(tmp5, tmp5, tmp1);
tmp2 = mad(tmp2, tmp2, 0);
tmp6 = mad(tmp6, tmp6, tmp2);
tmp3 = mad(tmp3, tmp3, 0);
tmp7 = mad(tmp7, tmp7, tmp3);
B[cb.s0] = tmp4;
B[cb.s1] = tmp5;
B[cb.s2] = tmp6;
B[cb.s3] = tmp7;
tmp0 = A[ca.s4];
tmp4 = B[cb.s4];
tmp1 = A[ca.s5];
tmp5 = B[cb.s5];
tmp2 = A[ca.s6];
tmp6 = B[cb.s6];
tmp3 = A[ca.s7];
tmp7 = B[cb.s7];
tmp0 = mad(tmp0, tmp0, 0);
tmp4 = mad(tmp4, tmp4, tmp0);
tmp1 = mad(tmp1, tmp1, 0);
tmp5 = mad(tmp5, tmp5, tmp1);
tmp2 = mad(tmp2, tmp2, 0);
tmp6 = mad(tmp6, tmp6, tmp2);
tmp3 = mad(tmp3, tmp3, 0);
tmp7 = mad(tmp7, tmp7, tmp3);
B[cb.s4] = tmp4;
B[cb.s5] = tmp5;
B[cb.s6] = tmp6;
B[cb.s7] = tmp7;Subgenerators rely on code managements features, and that's why it's strongly not recommended
to declare variables or functions bypassing the functions specially designed for that. If for example
kgenAddStmt() is bypassed, the infrastructure logic will simply not be able to resolve name
conflicts. In the same way, a function's opening/closing bracket should not be added
with inappropriate functions like kgenBeginBranch() or kgenAddStmt() because it will not allow body
functions declared lazily to be brought out. Therefore, all variables should be declared with
kgenDeclareVariables(), all functions should be declared with kgenDeclareFunction(), and all function
bodies should start with kgenBeginFuncBody() and ended with kgenEndFuncBody().